Для городов, являющихся крупными промышленными центрами и транспортными узлами, особое значение приобретают метеорологические измерения, в частности дальности видимости и скорости ветра. Потребителями информации об этих параметрах являются аэропорты, крупные транспортные магистрали, а также строительные, спортивные и другие хозяйственные объекты. Между тем, существующие приборы для измерения метеорологической дальности видимости (МДВ) и скорости ветра обладают определёнными погрешностями, связанными с недостаточной чувствительностью приборов, а также их инерцией (запаздывание измерения реальных значений величин во времени).
Цель исследования выявление возможностей совершенствования трансмиссометров и ротоанемометров с целью уменьшения их погрешностей, то есть увеличения чувствительности и уменьшения временной задержки измерений (инерции приборов).
Материал и методы исследования
При проведении исследования использован математический аппарат с составлением программы для персонального компьютера.
Результаты исследования и их обсуждение
Как известно [1–3], наиболее часто для измерения метеорологической дальности видимости используют трансмиссометры. Их принцип действия основан на ослаблении и последующем измерении яркости светового пучка, прошедшего определенное (базовое) расстояние в мутной атмосфере [4]. Таким образом, чувствительность S трансмиссометра может быть выражена как изменение отношения измеренной яркости светового луча J к исходному значению яркости луча, вышедшего из источника J0 при изменении МДВ (L) на один метр, то есть [1]:
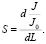 (1)
(1)
Для вычисления чувствительности используем уравнение Буге-Ламберта:
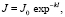 (2)
(2)
где k – показатель ослабления в мутной атмосфере, который описывается формулой Кошмидера:
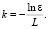 (3)
(3)
Здесь L – метеорологическая дальность видимости, ε – порог контрастной чувствительности глаза. Объединяя уравнения (2) и (3) имеем:
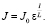 (4)
(4)
Дифференцируя (4), получаем выражение для чувствительности [2]:
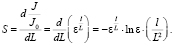 (5)
(5)
По полученной формуле (5) была проведена серия расчетов для выявления зависимости значения чувствительности трансмиссометра от его базы при разных значениях МДВ. Кривые на рис. 1 наглядно демонстрирует, что максимум для каждой кривой с увеличением МДВ смещается вправо и вниз, соответственно максимальная чувствительность снижается, и наблюдается при большем значении длины базы. С другой стороны (рис. 2), при постоянной длине базы чувствительность зависит от значения метеорологической дальности видимости и также имеет максимум, который при увеличении базового расстояния смещается в сторону больших значений МДВ [2]. Обращает на себя внимание, что все эти функции нормированы на единицу, то есть площадь, ограниченная графиками и осью абсцисс, одинакова и равна единице. Это легко понять, поскольку яркость потока меняется от J0 при l = 0 до нуля при l → ∞. Таким образом, семейство кривых (рис. 1) дает возможность подобрать наилучшее значение длины базы в зависимости от ожидаемых измеряемых значений МДВ. Кривые на рис. 2 дают возможность рассчитать погрешность измерения при выбранной длине базы.
Для более тщательного изучения соотношения между длиной базы и измеряяемой МДВ, найдем максимум фунции S(l) при постоянной L и S(L)при постоянной l. Приравняв нулю полученные значения получим условия максимума чувствительности [2]:
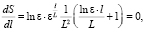 (6)
(6)
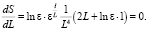 (7)
(7)
Из уравнения (6) получаем L = 3,5l, взяв ε = 0,03. А из уравнения (7) при том же значении ε – L = 1,75l. Полученнные соотношения позволяют сделать те же расчеты, что и по рис. 1 и 2, то есть найти оптимальныю длину базы, и вычислить погрешность измерения метеорологической дальности видимости.
Полученные значения чувствительности позволили рассчитать погрешность трансмиссометра. При проведении серии расчетов были использованы опубликованные технические характеристики импульсного фотометра ФИ-4. С их помощью рассчитана абсолютная погрешность измерения светового потока, которая в дальнейшем считалась постоянной [2, 5, 6]. Абсолютная погрешность измерения МДВ была получена с учётом чувствительности фотометра и её зависимости от дальности видимости.
Расчеты показали, что целесообразно изменять базу трансмиссометра в соответствии с наиболее характерной для данной местности мететорологической дальностью видимости. Например, при использовании трансмиссометров для обеспечения взлета и посадки воздушных судов, возможно привязать базу прибора к метеорологическуму минимуму аэродрома [2].
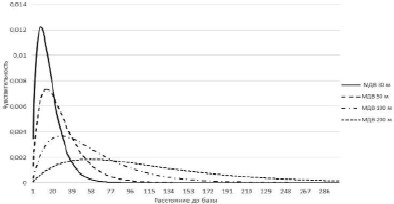
Рис. 1. Чувствительность трансмиссометра как функция расстояния, пройденного лучом, при разных значениях МДВ
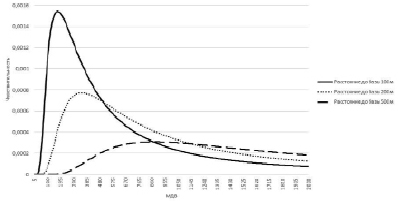
Рис. 2. Чувствительность трансмиссометра как функция МДВ при, разных значениях длины базы
Как известно, при измерениях скорости ветра ротоанемометры завышают среднюю скорость. Это завышение носит название «инерционная погрешность ротоанемометров» [1, 6, 7]. Как нам известно в настоящее время в литературных источниках нет сведений об исследовании инерционной погрешности, при проведении измерений предполагается, что она пренебрежимо мала. Серия проведенных расчетов показала, что это не совсем так.
Инерционная погрешность и время достижения анемометром стабильных показаний при различных скоростях ветра и его флуктуациях (рассматривались прямоугольные флуктуации) расчитывались по формуле (8).
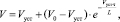 (8)
(8)
где Vуст – скорость ветра, которая будет воспринята анемометром (истинная);
V – текущие показания анемометра;
V0 – начальная скорость ветра;
L – путь синхронизации анемометра;
τ – время [1].
Для автоматизации расчётов и визуализации результатов (рис. 3), на языке программирования C Sharp (C#) была написана программа, позволяющая проводить большое количество расчетов за максимально короткое время.
Программа позволила исследовать и установить, что с увеличением средней скорости ветра инерционная погрешность анемометра возрастает [1]. При малых скоростях ветра (до 3 м/с) превышение незначительно и значением инерционной погрешности можно пренебречь. При скоростях ветра от 3 м/с до 5 м/с значение погрешности плавно возрастает, и при скорости ветра 6 м/с достигает нескольких метров в секунду. Такую погрешность учитывать уже необходимо.
Кроме того, чем больше амплитуда флуктуации скорости ветра, тем сильнее анемометр завышает скорость ветра, соответственно инерционная погрешность ΔV так же увеличивается. Если при изменении амплитуды флуктуаций от 0,1 до 1,5 м/с превышение можно не принимать во внимание, то при амплитуде флуктуаций более 2,5 м/с показания анемометра уже значительно завышают скорость ветра. При амплитуде флуктуаций в 6-7 м/с, погрешность составляет около 2 м/c.
Оказывает влияние на величину инерционной погрешности и период флуктуаций. При увеличении периода флуктуаций инерционная погрешность тоже возрастает. Также при удлинении периода флуктуаций возрастает время достижения стабильных показаний анемометра. При порывистом ветре время достижения стабильных показаний уменьшается с увеличением скорости ветра. Если при скорости ветра 3 м/с время восприятия составляет около 40 с, то при скорости ветра 10 м/c время восприятия уменьшается до 14-15 с.
Так же время достижения стабильных показаний анемометром уменьшается с увеличением амплитуды флуктуаций. Если при амплитуде 1-2 м/с оно составляет 40-45 с (рис. 4), то при резком порывистом ветре с амплитудой флуктуаций 20-25 м/c время достижения стабильных показаний составляет около 10 секунд.
Период флуктуаций также влияет на время достижения анемометром стабильных показаний. Понятно, что при удлинении периода флуктуаций время достижения стабильных показаний возрастает. Однако, по отношению к периоду флуктуаций оно практически не изменяется.
Увеличение пути синхронизации тоже оказывает влияние на величину инерционной погрешности (рис. 5), при этом время достижения стабильных показаний также увеличивается (рис. 6).
Расчеты показали, что при уменьшении скорости ветра инерционная погрешность остается такой же, как и при увеличении скорости, а время достижения стабильных показаний уменьшается. Впрочем, разница невелика и не превышает 2-3 секунд, что составляет 5-10 % по отношению в самой величине времени и поэтому может не учитываться при измерениях.
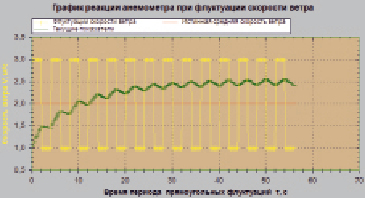
Рис. 3. График реакции анемометра на прямоугольные флуктуации скорости ветра
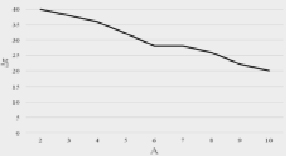
Рис. 4. Зависимость времени достижения ротоанемометром стабильных показаний от амплитуды флуктуаций скорости ветра
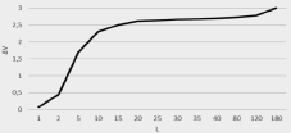
Рис. 5. Зависимость инерционной погрешности ротоанемометра от пути синхронизации
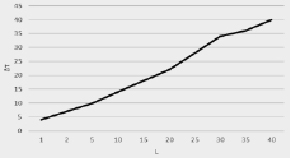
Рис. 6. Зависимость времени достижения ротоанемометром стабильных показаний от пути синхронизации
Заключение
Результаты исследования позволяют сделать вывод, что целесообразно изменять базу трансмиссометра в соответствии с наиболее характерной для данной местности значениями мететорологической дальности видимости.
Для уменьшения погрешностей ротоанемометров, целесообразно изготавливать их с малым путём синхронизации, то есть ротоанемометр должен обладать малыми размерами и малой массой. Полученные материалы могут быть использованы при проектировке анемометров и для автоматизированной обработки результатов измерений, то есть дают возможность автоматически учитывать и устранять инерционную погрешность.

