Scientific journal

European Journal of Natural History

ISSN 2073-4972

ИФ РИНЦ = 0,301

An idea of oscillator exists in quantum mechanics. Let us show, that the planet system really is a linked system of pendulums. A criterion of the platen orbits and the whole planet system steadiness can be the condition:

 T_j/T_ij = m + 1, (1)

where m = 1,2... is a whole positive number. For planets with the circulation period T_i and T_j (_Ti < T_j) the meeting period T_ij equals

 1/T_ij = 1/T_i + 1/T_j, or T_ij = (T_i∙T_j)/(T_i + T_j) (2)

If we substitute this equation into the initial one, we will obtain the oscillator equation:

 T_i = T_j/m. (3)

As T_j we will choose the period of the sun circulation around the system masses centre T_j = T_c and we will calculate m = T_c/T_i (table 1). Here T_i will be the Planets-Giants´ circulation period.

Table 1

The sun controls planets

Astronomers already refer Pluto to planets and this is confirmed by the fractional index m ≈ 3/4. For other planets this condition is accurately satisfied.

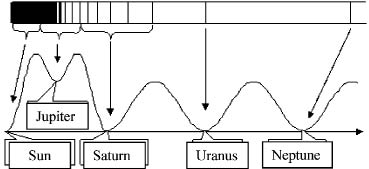
In table 1 index m runs through the values out of sequence, and that gives us grounds to suppose the final number of levels in system K = C/V_g = 22351 (this constant is responsible for the Universe structure). Here C is the light speed, V_g = (G_N-K∙G_K)^½ is the graviton speed, G_N-K is the constant of Newton-Cavendish, G_K is the «magnet» gravity constant, M₀ is the sun mass. In this case planets Neptune and Uranus are represented by one oscillator level each, and Saturn, Jupiter, and Sun level number is defined by the number of oscillator levels above each Sun gravity wave superposition holes - the graphic analogue of Schredinger equation (Figure and
table 2). The Sun main gravity wave length is λ₀ = M₀/G_K, and period T₀ = 2πλ₀/V_g = 10,95 years. The sun gravity potential is represented by the sum of two waves. The main wave with length equals λ₀ and is in same condition as wave with length 2λ₀ with three condition of the «spin» projections number. «Spin» is also a quantum analogue.

Table 2

The results of the Planets-Giants´ mass calculation

The mass of one oscillator level (gravity level) in system M_Ur equals:

M_Ur = M/K = 8,91∙1028 г,

here M is the Sun system mass

 M ≈ M₀ = 1,99∙1033 g. (4)

The observed Uranus and Neptune masses (М_U = 8,7∙10²⁸ g and М_N = 10,3∙10²⁸ g) corresponds to the oscillator level mass well. As all oscillator levels are identical, the other planet masses (and Sun) are defined by the number of oscillator levels above the corresponding gravity wave «hole». To put the obtained oscillator over the wave superposition the time is recalculated into the distance according to the Kepler law. The solar system has two energetic conditions. Jupiter is in the first condition, and Saturn, Uranus, and Neptune are in the second. The position of the Sun gravity potential is showed by Figure.

Therefore, the orbit radiuses, movement speeds, equator inclinations and masses of Planets-Giants are predefined by the Sun mass in the same way as the core charge defines the structure of atom electric cover.

Terrestrial planets were formed in the areas of the main wave interference (ℓ is a whole number):

 R = λ₀/(2∙ℓ + 1) (5)

is the orbit radius.

If we carry on the quantum mechanics analogy, the «gravity radiation constant» k in a similar way with the Plank constant and «spin» of planets in this index units will look like:

k = p∙λ₀

or

k = M∙V_g∙λ₀ = M²∙(G_N-K∙G_K)^½/G_K = = M²∙(G_N-K/G_K)^½ (6)

and

S_kg = (k/2π)∙m = (M²/2π)∙(G_N-K/G_K)^½∙m,

where m is the gravity «spin».

References

1. Kurkov A.A. Personal Internet - magazine. Registered on 02.06.2007 [digital source] / Science - News: site: URL: http://zaza149.inauka.ru/ (request date 13.01.2011).