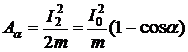
where ![]() - a body impulse. Under the same formula work of centripetal force pays off.
- a body impulse. Under the same formula work of centripetal force pays off.
From the law of inertia Galilee (Newton´s I law) follows, that any body shows resistance at attempts to set it in motion or to change the module or the DIRECTION of its speed. This property of bodies is called as inertness. To overcome resistance, it is necessary to make effort, i.e. to make work. The formula for calculation of work of change of speed of a body is resulted in all textbooks of physics. It is received on the basis of Newton´s II law for a resultant of force ![]() in a kind
in a kind
![]() (1)
(1)
As way ![]() it is possible to express work through an impulse of force
it is possible to express work through an impulse of force ![]()
![]() (2)
(2)
Let´s define work, which needs to be spent to change the DIRECTION of movement of a body, i.e. to turn a vector of speed V0 on some corner α. The author [1-3] named its WORK of TURN. At change of a direction of movement at ![]() kinetic energy of a body does not change, but work should be spent, as the body shows resistance to attempt to change a direction of its speed. Change of a direction of movement we will make at the expense of action of INSTANT FORCE F2 for what we will direct an interval of action of force t→0, and size of force F2 → ∞. Then we will receive instant force in the form of
kinetic energy of a body does not change, but work should be spent, as the body shows resistance to attempt to change a direction of its speed. Change of a direction of movement we will make at the expense of action of INSTANT FORCE F2 for what we will direct an interval of action of force t→0, and size of force F2 → ∞. Then we will receive instant force in the form of ![]() , where
, where ![]() - delta-function Diraka [4].
- delta-function Diraka [4].
Turn work
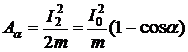 ,
, ![]() (3)
(3)
For corners of turn, big than ![]() , for example
, for example ![]() , considering periodicity of function
, considering periodicity of function ![]() , it is necessary to turn work on a corner 180о (Aπ ) to add work Aα. Kinetic energy of body
, it is necessary to turn work on a corner 180о (Aπ ) to add work Aα. Kinetic energy of body ![]() . In table 1 work of turn Aα depending on corner α is resulted.
. In table 1 work of turn Aα depending on corner α is resulted.
Table 1
|
α |
0° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
|
Aα |
0 |
|
|
K0 |
2K0 |
4K0 |
6K0 |
8K0 |
Thus, at turn of a body, moving on a circle, i.e. on one turn, work equal 8K0 (eight kinetic энергий bodies) is spent.
In textbooks of physics for force F directed under some corner α to moving S, the formula for moving work write down in a kind: ![]() . In this connection assert, that the centripetal forces causing movement of a body on a circle (for example, Lorentz´s force at rotary movement of a charge in a magnetic field, or force of gravitation at movement of the companion round the Earth on a circular orbit) do not make work, since they are always perpendicular to a vector of speed, and
. In this connection assert, that the centripetal forces causing movement of a body on a circle (for example, Lorentz´s force at rotary movement of a charge in a magnetic field, or force of gravitation at movement of the companion round the Earth on a circular orbit) do not make work, since they are always perpendicular to a vector of speed, and ![]() .
.
Companion movement is an infinite falling of a body by gravity. Companion movement to similarly movement of the body thrown from a tower in height in a horizontal direction with initial speed V0. At body falling to the Earth the gravity makes work ![]() . Not clearly, why the gravity does not make work at companion movement. These processes are similar.
. Not clearly, why the gravity does not make work at companion movement. These processes are similar.
In work [3] conclusion of the formula for calculation of work of centripetal force F by three methods. The formula (3) as a result turns out. As ![]() (3) it is possible to copy in the form of
(3) it is possible to copy in the form of ![]() . At
. At ![]() it is received
it is received ![]() - the usual formula for work, where S - the vertical moving equal to radius of an orbit. At one turn
- the usual formula for work, where S - the vertical moving equal to radius of an orbit. At one turn ![]() and work will be equal
and work will be equal ![]() .
.
References
- Ivanov E.M.work of centripetal and gyroscopic forces. // Bulletin DITUD, № 1:, Dimitrovgrad, 2003.
- Ivanov E.M. Work of centripetal and gyroscopic Forces. // European Journal History, 2006, №1, p.80.
- Ivanov E.M.work and energy in the classical mechanics and I law of thermodynamics. Dimitrovgrad: DITUD UlGTU, 2007.
- Arfken G. Mathematical methods for physics. Academic Press. New York and London.

