, where h - initial height of a body over a surface of the Earth, Vk - final speed. We will designate length of inclined plane S, and a corner of its inclination to horizon - α, then h = S • sin α. According to the law of conservation of energy, final speed will be same: and in case of vertical falling, and in case of sliding on an inclined plane: 
etc. It is said that the gravity in all cases has made same work mgh. We Will imagine, that corner α very is small. Then the body will appear on considerable removal from a place of vertical falling. Thus it will possess precisely same kinetic energy, as well as at vertical falling. At sliding on an inclined plane the body not only goes down to the Earth, but also moving work on considerable distance is made. Work at sliding should be more works at vertical falling.
At movement of a body without a friction on an inclined plane gravity P = mg can be spread out on two components: rolling force 
and normal reaction of support 
. The square of time of sliding on an inclined plane is equal 
.
Work of roll down forces
(1)
It is possible to express through an impulse rolling forces 
(1а)
Work of normal force we will write down through an impulse of force 
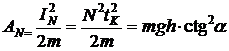(2)
Since forces 
and N orthogonal works of these forces are additive. Then total work of these forces can be found arithmetic addition
(3)
From (3) as the special case turns out gravity work at vertical falling (
): 
. At coal 
work of gravity 
.
If the inclined plane is rough, movement occurs to some factor of friction 
. We will consider a case of spontaneous sliding of a body (
). In this case uniformly accelerated sliding will occur downwards under the influence of force 
. Sliding time.
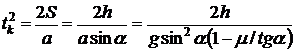(4)
Speed in the end of an inclined plane
(5)
The work made by a gravity, at sliding with a friction on an inclined surface.
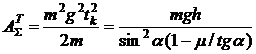(6)
At factor of friction 
we receive a parity (3). The relation of work with friction 
to work of gravity 
in the absence of a friction depending on relation 
are resulted in table 1.
Table 1
|
|
0 |
0,2 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
|
|
1 |
1,25 |
1,667 |
2 |
2,5 |
3,33 |
5 |
10 |
20 |
At factor of friction 
and coal work of gravity 
.
More detailed conclusion of formulas for calculation of work of various forces is resulted in [1,2].
References
- Ivanov E.M. Work and energy in the classical mechanics and the first law of thermodynamics. Dimitrovgrad: DITUD UlGTU, 2004.
- Ivanov E.M. Work of centripetal and gyroscopic Forces.//European Journal Natural History, 2006, #1, p.80.