Scientific journal

European Journal of Natural History

ISSN 2073-4972

ИФ РИНЦ = 0,301

Education includes several components. Naturally, on the first place, side by side with the training of morality, should be teaching of bases of studied discipline that have place at the codifier. But not less important role, and in authors´ opinion the principle role, should be played by the training of thinking. That means mastering and creation of innovations that are connected with the construction of adequate models of the visual environment and ourselves [1]. We can label non-linear equations (Navier-Stokes, Fokker-Planck, telegrapher) that are examined in the postnonclassical science synergy, power functions of Benua Mandelbrote, equations of Lotka-Volterra, equations of catastrophes´ theory to the perspective in modeling processes in physics, chemistry, biology, biophysics, conceptions of modern natural science, ecology etc.

Mathematical modeling is the constructive approach to the research of one or another behaviour of objects or systems. Thus in geophysics while the studies of behavior of ionize component of atmosphere, particularly at ionosphere, we examined the equations of Navier-Stokes [2]:

                 (1)

where N_i - concentration of particles [O⁺], [H⁺], [O₂⁺], [NO⁺], [Mg⁺] ; q - speed of ion formative, γ - coefficient interspecific interaction of particles; α - coefficient of recombination; div(N_iv) - diffusion term.

For hydrogen, for example, equation will be:

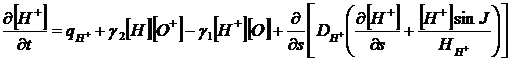,        (2)

where J - magnetic inclination.

Let´s add phrase for the temperature of ions to these equations:

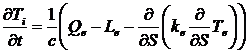,                           (3)

where k - coefficient of thermal conductivity.

The magnetic inclination J was taken from our model [2,3] of magnetic field of Earth, which is based on the equation:

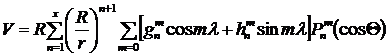,                    (4)

where V - magnetic potential, which is created on the distance h = r-R from the spherical surface of R radius that was caused by the source inside the sphere; g_n^m, h_n^m - coefficients of decomposition, P_n^m(cosΘ) - standardized added Legendre polynomials [2,3].

As the result we have distribution of parameters of magnetic field along the force tubes of Earth. These equations were solved numerically, with the method of marching on the implicit scheme. So far as these is the Cauchy problem we chose top and lower boundary conditions from the basis of force tube of magnetic field of Earth, initial conditions were taken from the experiment. Задача решалась до периодичности. The model of type (1) were used by us, for example, for the rating of contribution of innovative component into the education [1], for the rating of number of free radicals in the animal and human while the electronic excited conditions [2], for the creation of algorithm of more widen version of model "predator-prey".

Autowave processes in physics and biophysics were investigated at the example of Lotka-Volterra [2,4]:

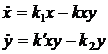 ,                  (5)

where  - speed of development of population of hares and pradators naturally;  - coefficients of reproduction; k и k₂ - coefficients of animal´s death.

Models of type (5) were used by us for the medical aims, for example, the model of humoral immunity with the delay helps us to define the ratio of antigen-antibody at different phase of disease, what allows injecting a medicine at the right time to the fast recovery.

No less innovative and interesting are models of fractals. In the capacity of easiest variant wes used model [5]:

,                      (6)

where D - fractal dimension; δ - step; N(δ) - the length of indented line; α - coefficient of inclination.

For the cluster one can use:

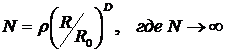,                      (7)

where ρ - density of mass; R₀ - minimal size of cluster.

Qualitative peculiarity of fractal objects is invariance of principle geometrical peculiarities of structures of wildlife and abiocoen while the scale changes.

Mathematic modeling of non-linear processes that occur in the open, equilibrium, dissipative systems, allows deeply learning of different kinds of phenomenons of our world, that promotes improvement of quality of preparation of specialists, ensuring the priopity development of theoretical researches in the institutions of higher education. All these give to students an opportunity of forming new type of thinking, which is directed at active, innovative transformations in the society, nature and technology.

References

1. Kutimskaya M.A., Buzunova M.U. The role of synergy in the system of education at the agrarian institute of higher education. / The system of education at the agrarian institute of higher education: problems and tendencies. Materials MNPK. - Irkutsk: publishing company IrGSHA, 2008. - P. 246-251.
2. Kutimskaya M.A., Volyanuk E.N. Bionoosphere: tutorial. - Irkutsk: Irkutsk´s university, 2005. - 212 p.
3. Kutimskaya M.A., Jozefaciuk G, Wrraszcz E, Buzunova M.U. Effect of magnetic fields and plants vital activity. /Physics in agricultural research. International Scientific Conference. Papers and short communication. - June 12-13, 2008, Lublin, Poland.
4. Haken G. Synergy. - Moscow: Peace, 1983.
5. Feder E. Fractals: Translation - Moscow: Peace, 1991. - 254 p.