Приоритетным направлением развития топливно-энергетического комплекса страны объявлено освоение углеводородных ресурсов Восточной Сибири и Дальнего Востока. Характерной особенностью данного региона являются специфические природно-климатические условия (вечная мерзлота, обводненность и заболоченность почвы), требующие проектирования и строительства магистральных трубопроводов как наземных сооружений, уложенных на специальные эстакады. Тем самым, актуальной прикладной задачей, наряду с традиционными вопросами обеспечения несущей способности трубопровода, выступает задача исследования устойчивости состояния покоя трубопроводной арматуры, то есть тех конструкционных узлов, которые обеспечивают защиту и удержание трубопровода в проектном положении [1]. К таким узлам относят как специализированные механические связи (поддерживающие опоры), так и демпфирующие устройства и компенсаторные узлы. Необходимо отметить, что вопрос об устойчивости равновесия возникает тогда, когда наложенные на объект связи закрепляют его не жестко, что зачастую объявляется как проблема нарушения технических условий эксплуатации конструкции. При этом целостных научных разработок, ориентированных непосредственно на описание и оценку технологических эффектов, проявляющихся в таких инженерных системах, явно недостаточно. Для эффективной эксплуатации нефтегазового промышленного оборудования и минимизации затрат на техническое обслуживание необходима своевременная и точная диагностика всех конструкционных узлов в процессе эксплуатации [2]. На этом основании заявлена целевая установка исследования, акцентирующая сущностное содержание прогностической диагностики как современного этапа развития технического диагностирования в целом.
Цель исследования состоит в разработке универсальной математической модели конструкционных узлов трубопровода, позволяющей сформировать вычислительный алгоритм условий прочности и устойчивости трубопроводной арматуры как теоретической базы выбора эффективных методов инженерной защиты трубопроводной системы.
Материал и методы исследования
Предметом исследования выбраны специализированная система защитных и поддерживающих опор, демпфирующие и компенсаторные устройства, обеспечивающие устойчивость состояния покоя магистральных трубопроводов [3].
В качестве общенаучной базы исследования используется фундаментальное знание теоретической механики, позволяющее организовать системный подход к решению инженерных задач технического диагностирования, а именно метод математического моделирования исследуемых явлений; базовые представления об устойчивости равновесия несвободного твердого тела; теорема Лагранжа – Дирихле как универсальное условие устойчивости состояния покоя механической системы с одной степенью свободы; принцип Ле Шателье – Брауна как фундаментальный принцип подвижного равновесия, применяемый к равновесию любой природы. Данный теоретический фундамент образует методологическую регулятивную систему инженерных исследований, регламентирующую выдвижение содержательных гипотез и установление математических закономерностей для описания эффектов равновесия (устойчивости).
Использованы следующие исследовательские методы: анализ действующих государственных стандартов нефтегазовой отрасли для обоснования проблемы и цели исследования; реферативное исследование специфики методик технического диагностирования; структурно-логический анализ конструкционных особенностей трубопроводной арматуры для выявления обобщенных технологических признаков.
Результаты исследования и их обсуждение
Предложенная теоретическая база исследования позволила оптимально выстроить последовательность мероприятий для достижения заявленной цели. В первую очередь формировалась обобщенная математическая модель конструкционного узла как методологическая основа изучения состояния устойчивого равновесия. Построение математической модели диагностируемого объекта выступает базовым основанием прогностической диагностики технических систем. При этом под моделью понимается описание объекта, позволяющее научно обоснованно выявить комплекс диагностирующих параметров. Прогнозирование по диагностическим параметрам относят к наиболее прогрессивному виду технической диагностики. Вместе с тем, необходимо отметить, что при техническом прогнозировании проблема выбора параметров диагностики является весьма специфической и сложной инженерной задачей, поскольку формализованных методов в этой области инженерии не существует. Зачастую диагностирующие параметры выбирают интуитивно на основе знания структурных особенностей, функциональных, механических, физико-химических свойств определенных объектов, учитывая условия их эксплуатации. В проведенном исследовании показано, что к разряду базовых параметров диагностики можно отнести физические величины, наиболее информативные по отношению к описанию математической модели диагностируемого объекта.
Для построения математической модели проведен анализ, классификация и обобщение принципов проектирования и технологических условий включения в трубопроводную систему следующих арматурных узлов: неподвижные и скользящие хомутовые опоры, трубчатые опоры, пружинные опоры, высоковязкий демпфер (патент SU1689693A1), сильфонный компенсатор [4]. В результате сделан вывод, что системным обобщающим признаком большинства технологических узлов выступает принцип конструирования «по типу ступенчатого цилиндра». Включение таких поддерживающих опор в структуру трубопровода осуществляется путем их сопряжения с выступом внешнего обода трубопровода «по типу катковой опоры с роликами» [5]. Если внешний и внутренний радиусы ступенчатого цилиндра обозначить r1 и r2 соответственно, то высота выступа основания крепления опоры h равна разнице радиусов ступенчатого цилиндра, т.е. h = r2 – r1.Совершенно очевидно, внешняя динамическая нагрузка на конструкционный узел будет вызывать эффект качения, что влечет потенциальную потерю устойчивости. Значит задача исследования устойчивости равновесия таких инженерных систем сводится к прикладной задаче обеспечения «условий не движения» ступенчатого цилиндра по такому же основанию. При этом радиусы цилиндра задают положение внутренней поверхности качения (обозначим 1) и внешней поверхности качения (обозначим 2).
Оптимизационный подход к построению математической модели физических явлений требует выявления и учета только базовых силовых факторов, что позволяет значительно уменьшить фактор случайности внешних и внутренних воздействий. Наиболее эффективной является аналитическая модель, в которой отсутствует зависимость будущего технического состояния от случайных помех и погрешностей. Такой подход позволил нам сформировать обобщенную математическую модель конструкционного узла. Опишем предлагаемую модель.
1. Представляется целесообразным выставить границы исследования эффекта возможного движения цилиндра как перемещение с постоянной скоростью. Такое ограничение спектра возможных движений объекта позволяет считать равнодействующую внешней динамической нагрузки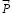 
(движущая сила), приложенной к оси цилиндра и направленной в сторону возможного движения. Вертикальная нагрузка 
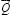, воспринимаемая опорой непосредственно от трубопровода, также рассматривается приложенной к оси цилиндра. Силы 
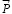и 
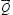формируют систему внешних силовых факторов.
2. Система внутренних силовых факторов ступенчатого цилиндра сформирована следующим образом. Во-первых, реакции связей, роль которых выполняют внутренняя и внешняя поверхности качения (обозначены в тексте как 1 и 2), фиксируются нормальными реакциями данных поверхносте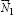й 
и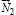 
. Анализ наиболее распространенных технологических проблем, возникающих при эксплуатации рассматриваемых конструкционных узлов (значительный нагрев, потеря устойчивости и др.) с наглядностью подтверждает наличие эффекта и трения качения, и трения скольжения как основополагающих факторов проявления жизнедеятельности конструкции [6]. Учет эффекта трения качения с необходимость требует показать приложение 
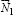и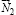 
в точках, отстоящих от вертикального диаметра на расстояниях k1 и k2 соответственно, где данные расстояния – коэффициенты трения качения по поверхностям 1 и 2. Учет сил трения скольжения фиксируется векторам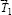и 
и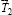 
, приложенными в тех же точках, что 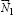и 
и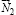 
и направленными вдоль поверхностей 1 и 2. При этом вектор 
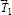направлен в сторону, обратную действия силы 
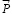, а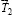 
направлен в сторону возможного качения как условие обеспечения движения ступенчатого цилиндра. Считая, что возможное скольжение будет на обеих поверхностях, для сил трения имеем следующие выражения: T1 = f1N1 и T2 = f2N2, где f1 и f2 – коэффициенты трения скольжения на поверхностях 1 и 2.
В результате группировки базовых силовых факторов сформирована обобщенная математическая модель конструкционного узла. На основании данной модели предложен алгоритм диагностики устойчивости равновесия арматурных узлов магистральных трубопроводов как метод установления соотношений между всеми силовыми факторами, при которых возможно равновесие конструкции. При этом мы работаем с классическим представлением об устойчивости равновесия как непременном условии возвращения объекта в положение равновесия всеми действующими на него силами, если он из этого положения выведен [7, с. 532]. Опишем предлагаемый алгоритм диагностики.
1. Фундаментальное знание теоретической механики об устойчивости равновесия несвободного твердого тела связывается с необходимостью обоснования, в первую очередь, вида механического движения исследуемого объекта, что позволит выяснить факторы потери устойчивости. Движение цилиндра по неподвижной поверхности – яркий образчик плоскопараллельного перемещения объекта. Такой вид механического движения относится к разряду частного случая в теории общего случая движения твердого тела, показывающей одновременность совершения объектом и поступательного перемещения со скоростью центра масс, и поворота вокруг оси, проходящей через центр масс.
Характерной особенностью теории плоскопараллельного движения является возможность его приведения к наглядной универсальной геометрической картине как движения мгновенно вращательного, осуществляемого по отношению к оси, проходящей через мгновенный центр скоростей тела. Наличие в инженерном искусстве представлений о мгновенной оси вращения позволило нам предположить, что базовым фактором потери устойчивости ступенчатого цилиндра выступает возможность вращения объекта под действием заданных сил вокруг мгновенной оси. Тем самым, задача исследования сведена к поиску в математической модели точки, через которую проходит мгновенная ось вращения.
2. Базовое знание теоретической механики об общем случае движения цилиндра вокруг мгновенной оси позволяет сделать однозначный вывод о том, что мгновенная ось располагается на вертикальном диаметре между поверхностями 1 и 2 на расстоянии y от первой. Совершенно очевидно, что y является характерным параметром, зависящем напрямую от всех силовых факторов – и внешних, и внутренних. Задачу получения уравнения устойчивого равновесия конструкционного узла предлагается решить с помощью составления условия равновесия несвободного твердого тела, имеющего неподвижную ось вращения z, проходящую через мгновенный центр скоростей тела. Условие равновесия тела состоит в том, что сумма моментов всех действующих сил относительно этой оси должна быть равна нулю. Тогда для предложенной математической модели имеем следующее выражение
P(r1 + y) – N1k1 – N2k2 – T1y – T2(r2– r1 – y) = 0.
Как видно из данного уравнения вертикальная нагрузка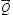 
исключается из факторов, оказывающих влияние на потерю устойчивости конструкционного узла. Равновесие исследуемого объекта будет устойчивым, когда величина момента движущей силы P будет равна или меньше вращающего эффекта всех остальных силовых факторов. Рассматривая это выражение относительно движущей силы P и обозначив постоянные
A = N1k1 + N2k2 – f2N2(r2 – r1),
B = f1N1 – f2N2
C = r1,
получим уравнение устойчивого равновесия
.
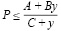Из полученного уравнения видно, что величина движущей силы напрямую зависит от положения мгновенной оси вращения цилиндра, фиксируемой параметром y. При этом «руководящую» смысловую роль в данном выражении играет коэффициент В.
3. Определяющее значение при выяснении диапазона проявлений коэффициента В имеет поиск критического значения В, при котором положение мгновенной оси будет безразличным, неопределенным, поскольку, на наш взгляд, такая конструкционная схема позволяет обеспечить действительное состояние устойчивости объекта. Данную задачу целесообразно решить с помощью классической теоремы Лагранжа – Дирихле – устойчивое состояние покоя системы находится в положении минимума ее потенциальной энергии. При этом предлагается модифицировать данную теорему и составить условие устойчивости состояния покоя исследуемого объекта по отношению к величине движущей силы Р, а не по отношению к потенциальной энергии конструкционного узла, поскольку потенциальная энергия объекта, расположенного на горизонтальной поверхности стационарного трубопровода, является величиной постоянной. В результате получим
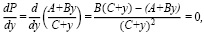
тогда
B(C + y) – (A + By) = 0
и Bкр = А / С.
Анализируя выражение для Bкр можно сделать вывод:
для обеспечения гарантированного не скольжения на поверхности 1, необходимо выполнение условия В > Bкр или
f1N1r1 > N1k2 + N2k2 + f2N2r2.
для обеспечения не скольжения на поверхности 2 должно выполняться условие В < Bкр или
f1N1r1 < N1k2 + N2k2 + f2N2r2.
4. Задачу выяснения границ проявлений y предлагается решить с помощью принципа Ле Шателье – Брауна, называемого еще принципом смещения равновесия. Центральная идея данного принципа – при внешнем воздействии, выводящим систему из состояния устойчивого равновесия, это равновесие смещается в направлении, при котором эффект внешнего воздействия уменьшается – позволяет говорить, что при возможном перемещении цилиндра затраты энергии на движение должны быть наименьшими, т.е. качение будет возможно при наименьшей величине движущей силы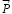 
. Это значит, что при y = 0 мгновенная ось будет располагаться на поверхности 1, при y = r2 – r1 мгновенная ось будет располагаться на поверхности 2. Формирование представлений о базовом факторе потери устойчивости конструкционного узла, связанного с функционалом параметра y в обобщенной математической модели, необходимо, в первую очередь, для получения целостной физической картины исследуемого явления устойчивости равновесия. Тем самым, концептуальный аспект алгоритма диагностики трубопроводной арматуры приобретает характер комплексности теоретического исследования. Технологический аспект как программа мероприятий дальнейших исследований предполагает организацию экспериментальной проверки полученных теоретических результатов на базе динамических методов исследования устойчивости равновесия, сущностное содержание которых формирует фундаментальное знание теоретической механики [7, с. 496].
Заключение
Полученные результаты показали, что определяющими параметрами диагностики состояния конструкционных узлов трубопроводов выступают характеристики эффектов трения скольжения и трения качения – коэффициенты соответствующих законов трения f и k. Данное заключение позволило сделать теоретическое исследование положения возможной мгновенной оси вращения, фиксируемое параметром y в предложенной математической модели конструкционного узла. Тем самым, задача обеспечения устойчивости конструкционных узлов магистральных трубопроводов напрямую связана с необходимостью изучения всех особенностей явления трения, проявляющихся в данных инженерных системах. Такой подход позволит сформировать комплекс научно обоснованных рекомендаций по техническим условиям изготовления большинства арматурных узлов, а именно – выбор материала, характера обработки, температуры и влажности среды использования, смазки внутренних элементов и др.
Практическая значимость исследования заключается в возможности использования полученных теоретических результатов при решении актуальных прикладных задач диагностики и инженерной защиты трубопроводной арматуры, что позволяет наиболее эффективно, на наш взгляд, обеспечивать устойчивость и безопасность магистральных трубопроводов.