Погода и её прогноз, в частности знание скорости ветра, над морскими акваториями приобретает особое значение для крупных транспортных узлов, в которых водный транспорт занимает не последнее место: приходят круизные лайнеры, паромы, сухогрузы; транзитом проходят целые караваны судов. Чем точнее будут проведены измерения скорости ветра и оперативно обработаны данные, тем точнее будет составлен прогноз. В свою очередь, своевременный и точный прогноз угрозы возникновения сгонно-нагонных явлений, приводящих к наводнениям, позволяет сократить простой судов, минимизировать финансовые потери и возможные риски, возникающие при приостановке навигации. Таким образом, качество и своевременность прогноза напрямую зависит от точности измерений и результатов обработки полученных данных. Кроме того, следует учесть, что потребителями метеорологической информации о скорости ветра являются и другие субъекты хозяйственной деятельности: строительные и спортивные объекты, отрасли дорожного, железнодорожного, водного и воздушного сообщения и другие [1, 2, 3].
Получить точные, репрезентативные данные о погодных условиях над морской поверхностью достаточно сложно. Ликвидировать пробелы в поступающей метеорологической информации может использование буйковых автоматических метеорологических станций, оборудованных необходимым комплектом датчиков. Такие станции устанавливаются непосредственно на водной поверхности в местах, где сложно получить информацию непосредственно контактными измерениями. Станции фиксируются с помощью специальных якорей и оснащаются блоком долговременного электропитания [4, 5, 6]. В то же время известно, что датчики скорости ветра (ротоанемометры), установленные на морских буйковых метеорологических станциях, обладают определёнными погрешностями, среди которых одна из основных – инерционная погрешность (завышение значения средней скорости ветра, измеряемой прибором, при колебании его под действием волнения поверхности моря) [7].
Цель исследования выявление и учёт инерционной погрешности ротоанемометров в зависимости от конструкции измерителя скорости ветра, буйковой станции, а также от параметров ветра, частоты и амплитуды волнения поверхности моря.
Для достижения поставленной цели необходимо решить ряд задач:
Провести расчёт инерционной погрешности ротоанемометров, установленных на морских буйковых метеорологических станциях, в зависимости от параметров ветра при определённых значениях высоты установки датчика;
Рассчитать инерционную погрешность ротоанемометров, установленных на морских буйковых метеорологических станциях, в зависимости от частоты и амплитуды волнения водной поверхности при заданных значениях скорости ветра и высоты установки датчика;
Подготовить рекомендации для автоматической компьютерной обработки результатов измерений скорости ветра с учётом инерционной погрешности.
Материалы и методы исследования
При проведении исследования использован математический аппарат с составлением программы для персонального компьютера.
Результаты исследования и их обсуждение
Буйковые автоматические метеорологические станции (АМС) представляют собой один или несколько буев с автоматическими метеорологическими датчиками для измерения скорости и направления ветра, температуры и влажности воздуха, атмосферного давления, количества осадков и облачности. Такие станции также измеряют характеристики водной среды – скорость течения, солёность, мутность и т.д. Очевидно, что буйковые АМС не дают полных сведений о погоде, а передают только информацию о состоянии атмосферы вблизи водной поверхности. Однако, эти станции очень важны, поскольку данные, полученные с них, позволяют заполнить пробелы в информации, приходящей с остальных средств наблюдений в море. [4, 5, 6].
Как видно из рис. 1, датчик скорости ветра устанавливается на некоторой высоте над поверхностью моря для того, чтобы исключить забрызгивание насколько это возможно. Однако, морской буй подвержен влиянию волнения моря. Легко понять, что датчик при этом совершает колебания в направлении скорости ветра. Таким образом, при движении датчика в направлении скорости ветра он регистрирует заниженную скорость, а при движении в направлении против скорости ветра – завышенную скорость. Следовательно, средняя скорость ветра будет определена с ошибкой, которую можно рассчитать, используя методику, разработанную и развитую в работе [8].

Рис. 1. Буйковая метеорологическая станция PIRATA (США, Франция, Бразилия)
Для проведения расчёта необходимо знать несколько величин – высоту датчика над уровнем моря, угловую амплитуду и частоту колебаний датчика. На рис. 2 представлено схематичное изображение колебания датчика под действием морских волн.
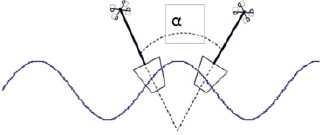
Рис. 2. Схематичное изображение колебаний датчика параметров ветра под действием волнения моря
Если H – высота, на которой располагается датчик, α – угловая амплитуда колебаний датчика, а T – период колебаний, то скорость передвижения датчика относительно поверхности моря может быть определена по формуле:
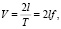 (1)
(1)
где l – длина дуги, на которую опирается угол α;
f – частота колебаний (Гц).
Длину дуги определим по формуле:
l = αH, (2)
где α – угол в радианах.
Согласно теоретическим сведениям, частотный диапазон морских волн может варьироваться от 0,07 до 8 рад/с, т.е. от 0,011 до 1,25 Гц. Соответственно период колебаний буя составляет от 0,5 до 10 с. Углы отклонения, согласно [9], могут изменяться в пределах от 40 ° до 68 °, т.е. от 0,7 до 1,2 рад.
При установке датчика параметров ветра на буйковую автоматическую метеорологическую станцию используются две стандартные высоты H1 = 2,9 м, H2 = 3,5 м. Значения высоты установки датчика H приводятся в [10]. Эти значения и были использованы при расчётах погрешностей.
В первую очередь необходимо рассчитать скорость движения датчика при разных значениях α и f для двух значений высоты датчика. Расчёты выполнялись по формуле (1) с учётом (2). Далее на основании полученных данных рассчитывались погрешности.
Для удобства расчётов флуктуации ветра были приняты прямоугольными. Расчёты производились по формуле (3) [7, 8]:
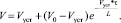 (3)
(3)
По методике, развитой в работе [8], определялась инерционная погрешность при заданных значениях скорости ветра, периода и амплитуды флуктуаций скорости ветра, пути синхронизации анемометра, который, как известно [7], характеризует инерцию анемометра и зависит от массы и радиуса чашек вертушки.
По результатам расчетов были построены графики зависимостей V(α) для трёх крайних значений частот f1 = 0,011 Гц, f2 = 0,5 Гц, f3 = 1,25 Гц [4]. Расчёты были выполнены для стандартных высот H1 = 2,9 м, H2 = 3,5 м. Результаты выполненной серии расчетов представлены на рис. 3 и 4.
Прежде всего стоит отметить, что в случае f1 = 0,011 Гц (сплошная кривая на рис. 3 и 4) скорости движения датчика оказались столь малыми, что рассчитанное значение погрешности для всех углов составляет доли см/с. Эта величина может считаться пренебрежимо малой, поэтому результаты расчёта для этого случая не включались в итоговую таблицу.
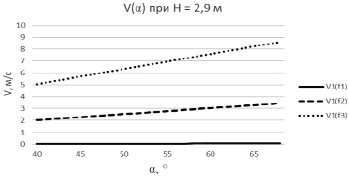
Рис. 3. График зависимости скорости движения датчика при разных значениях частот и углов раскачки буйковой станции
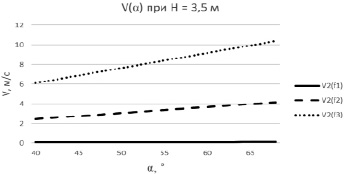
Рис. 4. График зависимости скорости движения датчика при разных значениях частот и углов раскачки буйковой станции
Для двух других случаев при частоте колебаний датчика параметров ветра f2 = 0,5 Гц, f3 = 1,25 Гц погрешности оказались достаточно значимыми (табл. 1 и 2).
Таблица 1
Результаты расчётов погрешностей для высоты датчика H = 2,9 м
|
Т, с |
α, ° |
Скорость движения датчика, м/с |
Скорость ветра, м/с |
Погрешность, м/с |
|
2 |
40 ° |
±2 м/c |
5 м/c |
1,45 м/c |
|
10 м/c |
0 м/c |
|||
|
20 м/c |
0 м/c |
|||
|
60 ° |
±3 м/c |
5 м/c |
1,1 м/c |
|
|
8 м/c |
0,25 м/c |
|||
|
10 м/c |
0,1 м/c |
|||
|
15 м/c |
0 м/c |
|||
|
68 ° |
±3,4 м/c |
5 м/c |
1,7 м/c |
|
|
8 м/c |
0,85 м/c |
|||
|
10 м/c |
0,15 м/c |
|||
|
15 м/c |
0 м/c |
|||
|
Окончание табл. 1 |
||||
|
Т, с |
α, ° |
Скорость движения датчика, м/с |
Скорость ветра, м/с |
Погрешность, м/с |
|
0,8 |
40 ° |
±5,06 м/c |
6 м/c |
4,03 м/c |
|
10 м/c |
1,5 м/c |
|||
|
15 м/c |
0,65 м/c |
|||
|
20 м/c |
0,33 м/c |
|||
|
25 м/c |
0 м/c |
|||
|
60 ° |
±7,5 м/c |
8 м/c |
6,75 м/c |
|
|
10 м/c |
4,2 м/c |
|||
|
15 м/c |
1,75 м/c |
|||
|
20 м/c |
0,6 м/c |
|||
|
25 м/c |
0,25 м/c |
|||
|
30 м/c |
0 м/c |
|||
|
68 ° |
±8,6 м/c |
9 м/c |
7,8 м/c |
|
|
10 м/c |
6,3 м/c |
|||
|
15 м/c |
2,3 м/c |
|||
|
20 м/c |
0,8 м/c |
|||
|
25 м/c |
0,3 м/c |
|||
|
30 м/c |
0 м/c |
|||
Таблица 2
Результаты расчётов погрешностей для высоты датчика H = 3,5 м
|
Т, с |
α, ° |
Скорость движения датчика, м/с |
Скорость ветра, м/с |
Погрешность, м/с |
|
2 |
40 ° |
±2,4 м/c |
5 м/c |
1,4 м/c |
|
10 м/c |
0,35 м/c |
|||
|
15 м/c |
0,15 м/c |
|||
|
20 м/c |
0,1 м/c |
|||
|
25 м/c |
0 м/c |
|||
|
60 ° |
±3,6 м/c |
5 м/c |
2,5 м/c |
|
|
10 м/c |
0,9 м/c |
|||
|
15 м/c |
0,25 м/c |
|||
|
20 м/c |
0,1 м/c |
|||
|
25 м/c |
0 м/c |
|||
|
68 ° |
±4,1 м/c |
5 м/c |
3,1 м/c |
|
|
10 м/c |
1,1 м/c |
|||
|
15 м/c |
0,4 м/c |
|||
|
20 м/c |
0,1 м/c |
|||
|
25 м/c |
0 м/c |
|||
|
0,8 |
40 ° |
±6,1 м/c |
8 м/c |
3,95 м/c |
|
10 м/c |
2,45 м/c |
|||
|
15 м/c |
1,05 м/c |
|||
|
20 м/c |
0,3 м/c |
|||
|
25 м/c |
0 м/c |
|||
|
60 ° |
±9,1 м/c |
10 м/c |
8,9 м/c |
|
|
15 м/c |
2,55 м/c |
|||
|
20 м/c |
1,05 м/c |
|||
|
25 м/c |
0,55 м/c |
|||
|
30 м/c |
0,15 м/c |
|||
|
35 м/c |
0 м/c |
|||
|
68 ° |
±10,3 м/c |
15 м/c |
5,35 м/c |
|
|
20 м/c |
1,65 м/c |
|||
|
25 м/c |
0,65 м/c |
|||
|
30 м/c |
0,15 м/c |
|||
|
35 м/c |
0 м/c |
Анализируя данные табл. 1 и 2, необходимо отметить, что в них отражены все возможные комбинации углов отклонения буя, скорости ветра и периода раскачки (или частоты). Поэтому в таблице могут встречаться явно нереальные случаи – например, при малой скорости ветра период колебаний не может быть очень большим из-за малой высоты волн, и, наоборот, при большой скорости ветра период колебаний не может быть малым.
Погрешность измерения, указанная в последнем столбце табл. 1 и 2, всегда означает превышение показаний анемометра над истинной средней скоростью ветра. Причина появления этого превышения указана в работе [8]. Разумеется, на эту погрешность накладываются другие погрешности анемометров, которые остаются за рамками данной работы.
Обращает на себя внимание, что величина погрешности особенно значительна при малых скоростях ветра. Это объясняется тем, что скорость раскачки буя сопоставима со скоростью ветра, а в некоторых случаях может даже превышать её. При больших скоростях ветра влияние скорости раскачки становится незначительным, и ошибка стремится к нулю.
Из табл. 1 и 2 также видно, что при прочих одинаковых условиях погрешность возрастает при увеличении высоты установки датчика. Это легко объяснить, т.к. с увеличением высоты увеличивается скорость раскачки буя. Таким образом, можно рекомендовать уменьшение высоты положения датчика. Впрочем, это может привести к забрызгиванию датчика водой и искажению показаний из-за измерения скорости ветра вблизи уровня шероховатости.
Заключение
Результаты проведённых расчётов могут быть использованы для автоматической обработки результатов измерений. В самом деле, океанографические буи оснащены датчиком частоты и угла раскачки [10] Знание этих величин позволит применить разработанную методику при определении истинной средней скорости ветра, заложив её в программу автоматической обработки измерений.

