Probabilistic-statistical methods are widely used, when conducting a scientific research. There are classical probabilistic-statistical method (CPS-method) and non-classical probabilistic-statistical method (NPS-method) [1]. CPS-method, based on the use of theory of probability and mathematical statistics, has wide application in the analysis of mass phenomena of a random nature [2]. The NPS-method of scientific research in contrast to the CPS-method could be used to study each particular event of a random nature.
Non-classical probabilistic-statistical method can be used to analyze human behavior in the process of an activity. Here we consider the use of the NPS-method for studying student behavior in the process of gaining knowledge.
Materials and research methods
In the process of learning individual moves in the information space, which represents the results of human semantic activity. Knowledge, that student acquire, has a random factor, since it is a product of consciousness, which determinism is realized through randomness [3]. This behavior of the student is a reflection of the internal properties, specific for each individual and conditioned by the random character of his mental and somatic state. This, for example, was the reason for the refusal from a deterministic dynamical model in favor of a random dynamical system in the modeling of human cognitive processes [4].
Since the process of assimilating knowledge involves a random factor, it is impossible to specify student’s precise position in the information space, we can only talk about the probability of its location in a specific area of space. This means that to describe student behavior in the process of assimilating knowledge, the non-classical probabilistic-statistical method can be applied. According to this method a student is identified with a distribution function in the information space, namely, with a probability density, which defines the probability to find an individual in a unit area of the information space.
The work [3] presents a system of continuity equations, associating partial time derivative of the probability density with the divergence of the probability density flow:
,
,
……………………………………………………………….,
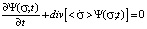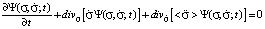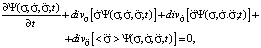
where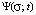 
, 
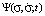and 
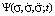are distribution functions, which identify a student in the information space; σ, 
, 
, 
, 
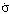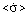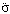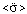and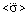 
are coordinate, velocity, average velocity, acceleration of the first order, average acceleration of the first order and average acceleration of the second order respectively; t is time.
This system consists of an infinite number of differential equations. To solve them one needs to have data on the average values of velocity and accelerations of various orders. The first and second equations from the above system of differential equations allow to find analytically from the known initial and boundary conditions the explicit form of the distribution function for any moment of time. Differential equations of higher orders can, possibly, be solved only by a numerical method.
It is notable that the random character of human behavior when he performs any activity to some extend is identical to the behavior of microparticles (for example, electrons, atoms, molecules etc.). Specifically, according to the Copenhagen interpretation of quantum mechanics the non-classical probabilistic-statistical method is also used to describe the behavior of microparticles. Microparticle is identified with a wave function, that is a solution of the Schrödinger equation. The wave function itself doesn’t have physical sense, but the square of the wave function does have and defines, under normalization condition, the probability density of finding a microparticle in the targeted area of the information space. It should also be noted, that the Schrödinger equation could be transformed to the continuity equation [5], which is similar to the first equation from the above system of differential equations.
Quantum-mechanical description of a microparticle system behavior is based on the principle of “indistinguishability”, all particles (for example, electrons) are identic and cannot be distinguished from each other. However, in case of describing the behavior of a student system it is necessary to use the principle of “distinguishability”, whereby each student has individual properties, that distinguish him from each other. In addition, the above system of equations allows taking into account the random location of the individual not only in the coordinate space, but also in the spaces of velocities and accelerations of various orders. Hence, the concerned NPS-method opens opportunities for the study of human behavior in various contexts.
When carrying out pedagogical measurements, scaling is of great importance. It is notable, that classical scaling methods cannot be used for measuring the completeness of a student’s knowledge, since they do not take into account the probabilistic-statistical character of student behavior. This problem can be solved by applying the non-classical probabilistic-statistical scaling method. According to this method the measurement scale is an ordered system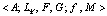 
, where A is some ordered set of objects (students), that have characteristics of interest to us (empirical system); LΨ – functional space (space of distribution functions); F is mapping of A to a subsystem LΨ; G is a group of admissible transformations; f is mapping of distribution functions from the subsystem LΨ to the numeric systems with relations of n-dimensional space M.
This measurement scale allows, when assessing the completeness of student’s knowledge, to pass from the functional space to the numeric space. For this purpose, student’s empirical distribution functions, received form the results of a review work, for example, an examination, are mapped onto the numeric space in the form of moments of different orders of these functions, obtained by calculation. Mostly it is enough to calculate the moments of the first, second and third orders, which characterize the mathematical expectation, dispersion and asymmetry of the distribution functions respectively.
Comparison of the moments of different orders of students’ individual distribution functions allows to rank students by the level of knowledge. The matter of the application of probabilistic-statistical scaling to measurements in pedagogy and to the assessment of student’s knowledge completeness, as well as student ranking by the level of knowledge, is clarified in [3]. Let us analyze some features of the experimental distribution functions.
Research results and discussion
In some cases the use of traditional five-point measurement scale for finding the experimental distribution function, identifying student, is not practical, since due to the large error of ±0,5 points and narrow scale range it is impossible to observe the true form of the individual distribution function (its fine structure is masked by an error). However, in some cases, when it is necessary to analyze simultaneously a large number of students, for example, a student batch, a five-point measurement system can be used, and in this case the true individual distribution function can be approximated by a rectangular distribution function, which width is equal to 1 point. This wouldn’t significantly affect the structure of the distribution function, that characterize the behavior of the student batch as a whole.
The use of point grading scales of higher orders, for example, a 20-point or a 100-point scale, allows to recognize specifics of the structure of individual distribution functions. So, fig. 1 shows typical individual distribution functions, obtained experimentally using a 20-point scale.
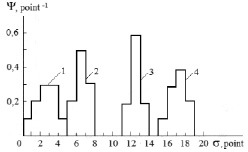
Fig. 1. Typical individual distribution functions of students, who have received in the physics exam traditional grades: 1 – “2” (unsatisfactory); 2 – “3” (satisfactory); 3 – “4” (good); 4 – “5” (excellent)
Individual distribution functions, shown in fig. 1, are in fact histograms, that can hardly be approximated with smooth lines. However, this can easily be done when statistically processing a large number of individual distribution functions, especially, using a 100-point measurement system. It is notable that the area under each individual distribution function is equal to one, since it corresponds to the probability to find a student in the entire information space.
As the order of measurement scale tends to infinity the individual distribution functions will come close to the true functions. However, none of the “true” individual distribution functions will be exactly identic to any other function in form and position in the information space, even for the student “clones”, that have completely the same initial properties. This due to the fact that the behavior of each individual student in the process of assimilating knowledge involves random factor. Here we find an analogy with the behavior of quantum microparticles, “clones”, that are prepared hypothetically in completely the same way. In quantum mechanics it is shown, that such microparticles, when passing, for example, through a slit, will with a certain probability fall into some or other area of the screen, and the probability of microparticles hitting one and the same point on the screen is zero.
On the basis of statistical processing of students’ individual distribution functions, distribution functions of the student batch were built (fig. 2). Individual distribution functions were rectangular functions with a width of 1 point, that were obtained experimentally using a five-point measuring system. It follows form the analysis of evolution of distribution functions, shown in fig. 2, that as functions move through the information space their dispersion increases and mathematical expectation shifts from the left bound towards the center. Over time, this leads to overlapping of the distribution functions, which becomes notably significant in senior years. This means, that the amount of knowledge of a strong junior student, can actually exceed that of a weak senior student. The overlapping of functions already becomes significant for the distribution functions, corresponding to the second and third course years. Thus, starting from the third year of study, student batch becomes markedly heterogeneous in terms of the level of knowledge, and learning efficiency in such groups decreases.
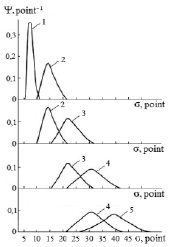
Fig. 2. Experimental distribution function of the student batch, found after the first year of study (curve 1), second year (curve 2), third year (curve 3), fourth year (curve 4), fifth year (curve 5)
Teachers, who conduct classes for the large student groups, in this case have to orient towards “average” students, this negatively affect the study of “weak” and “strong” students: weak students cannot sufficiently learn the material, and the potential of the strong students is not fully utilized. This leads to the increase in heterogeneity of student body and, therefore, to a reduction of the requirements for student attestation, which inevitably leads to the overall decrease in qualification of the intended specialists. In this context it is reasonable to move to the staged education with branching to enhance the efficiency of the educational process. This principle can be used for the optimization of the structure of higher educational system.
In Russian Federation the two-tier system of higher education actually takes place: bachelor’s degree (four years of study) and master’s degree (two years of study), while maintaining the specialist program. Such structure of the higher education system undoubtably improves the quality of student education. At the same time, it involves internal conflicts, conditioned by high heterogeneity of students in terms of the level of knowledge, that already appears after the second year of study (distribution function, identifying a student batch, already have high dispersion). The above analysis of the evolution of the distribution function of the student batch (fig. 2) showed significant overlapping of the distribution functions after the second and the third years of study. Hence, a stage of education should not last more than two years. This means, that bachelor’s program should be carried out in two stages with the allocation of quasi-homogeneous (in terms of the level of knowledge) student subsystems on each stage followed by branching with the aim of their separate study [6]. The principal of staged education with branching could be implemented in the structure of bachelor’s program in the following form (fig. 3).
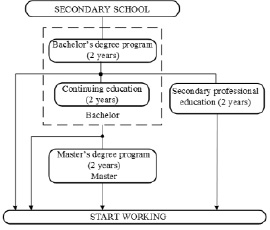
Fig. 3. An alternative structure of the higher education system, which takes into account the principal of staged education with branching in the structure of baccalaureate
It is hoped, that the proposed structure of the baccalaureate will allow to enhance the efficiency of the educational process, since after the first two years branching should take place, according to which only average and strong students will be able to continue study on the bachelor program, whereas weak students should be taken out of the bachelor’s program to continue study during 1,5-2 years on the specialist program, that corresponds to the secondary professional education (accountant, nurse, technician and etc.). It is supposed that on the first stage of education students should study fundamental and general disciplines and, upon successful completion, obtain a certificate, confirming of the stage completion. Such baccalaureate structure offers additional opportunities for student mobility, for example, to complete education after the first stage of baccalaureate and start working, to continue education on a bachelor’s program or program of specialist with a secondary professional education, as well as to pass to another higher educational institution and continue education there. After graduation from the bachelor’s degree the second branching takes place, according to which a graduate can start working or continue education in a master’s degree for 2 years.
Conclusion
In conclusion, we note that non-classical probabilistic-statistical method of scientific research takes into account the properties, specific for each individual and conditioned by random character of mental and physical state, and allows build a mathematical student model, according to which he is identified with a distribution function, that moves in the information space, and the analysis of experimental distribution functions makes it possible to rank students by the level of knowledge and to formulate the proposals for optimization of the educational process.