Modernization of education within basic link – school of general education – implies creating conditions for improving quality of general education through usage of effective training methods, establishing differentiation and individualization of education, introduction of pre-profile and profile training, system of state education quality evaluation, etc. Modernization of general education on the whole includes reformation of mathematical education.
The ability to perceive the worlds around us, act adequately to the received data, creating benefit for people, is an important characteristic of an educated person, whose responsibility for preserving civilization grew significantly during recent times.
Correspondingly, social expectation of our society consists in formation of a new type of person that has adequate social and methodological settings, has mastered cognitive methods and means, has a need and readiness to find solutions to problems of different level of complexity.
Efficiency and effectiveness of the found solutions and made decisions depends significantly on level of a specialist’s cognitive skills, including research skills. The importance of problem of forming these skills is supported by analysis of a large number of professiograms among specialists that we undertook. Each of them included the following necessary skills: undertaking researches, formulate and solve problems, take responsibility for the made decision. These skills are invariant, they allow us to determine level of professional and social competence of a specialist.
In this regard we can conclude that research skills should become an object of close attention for methodic scientists within process of preparing a person for professional and social activity.
Improvement of educational process nowadays follows the direction of active training methods that provide for a deep penetration into the essence of the studied problem and intensify personal involvement of each student and their interest in training.
One of the most important personal qualities of students is their ability to undertake training research, during which they obtain new knowledge and methods of activity.
Research activity of students nowadays obtains a role of utmost significance. It is defined by the fact that it is important during training period as well as later – in further professional activity.
Normative documents in field of education of Russian Federation outline: “New school is in institute that corresponds to objectives of overtaking development. In schools conditions will be established that provide not only for studying of former achievements, but also technologies that will be in use in future. Children will be involved into research projects and creative classes so that they learn to invent, understand, and master the new, express their own thoughts, make decisions, and help each other, formulate interests and realize their abilities” [1].
The developing function of research activity on mathematics consists in fact that during its process mastering methods and way of thinking, typical for mathematics, happens, as well as development of a conscious attitude towards one’s own experience, formation of creativity features and cognitive interest towards different aspects of mathematics.
Psychological-pedagogic research show us convincingly that all cognitive processes develop effectively when educational process is organized according to principle of involvement of students into researching activity.
Research activity is one of many forms of creative activity, therefore, it should be studied as a component within problem of developing creative abilities of students.
Development of a student’s personality, their intellect, feelings, and willpower happens only within activity. Human psyche does not only display, but also form within activity, but it cannot develop outside of activity. In form of neutral-passive perception one cannot form solid knowledge, deep ideas, and flexible skills.
Ability of students to create (therefore, to research) develops effectively in process of their purposeful activity under supervision of tutor.
It is necessary to create conditions that will provide for emergence of cognitive demand for new knowledge among students, as well as for mastering methods of its usage, and for creative activity that will influence formation of new skills.
Research objective
In this article we will demonstrate how the above-mentioned conditions can be formed through proving the known law of sines via different method.
In school courses on geometry, for example, in textbook [2] proof of law of sines is presented. Proving for this law can be also found in university textbooks on geometry, for example, [3].
Within this article we shall present author’s proof to law of sines that differs from the known proving.
Materials and methods of research
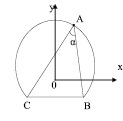
Let us study one of two arcs that emerge from diving a given circle by a given chord. From any point A of the selected arc the chord is seen under the same angle (it is considered that point A does not coincide with ends of the chord). In this note this fact is established via vector-coordinal method. The following labeling is used: R for circle radius, a for chord length, α for measure of angle A,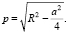 
There is a well-known case when chord is diameter (a = 2R), therefore later we suggest that it is shorter than diameter. Then one of two arcs is longer than the other, and we see it in fig. 1.
In case a) A is placed on the bigger arc, in case b) it is placed on the smaller arc.
From the figure we can see how coordinate system was selected – it begins in circle center, axis of absciss is parallel to chord BC.
Research results and discussion
Let us prove the following statement:
Lemma. There is an equality
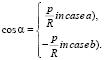(1)
Proof
Let us study case a) – point A is located on the bigger arc. For the identified system of coordinates we have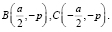 
Let 
where parameter t is selected so that
yA > yB⇔R sin t + p > 0 (2a)
Let us study vectors.
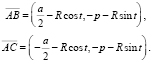
а) b)
Fig. 1. Illustration to proof of lemma
Let us find their scalar product. Omitting calculation details, we present the solution:
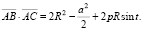
Then let us find squares of vector lengths:
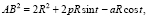
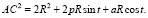
Their product equals
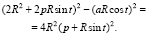
Therefore,
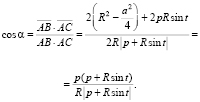
Since expression in round brackets is positive, we receive equality (1) for the case a).
In case b) we have inequality
R sin t – p > 0 (2b)
And equalities
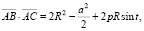
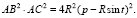
This time
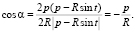
Lemma is proven. Let us provide examples of implementing equality (1). Note: it is true for a = 2R.
1. From (1) we see that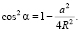 
Therefore,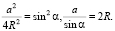 
By implementing this equality to two other sides of triangle ABC (fig. 1), we receive law of sines: relations of side lengths to sines of opposite angles is same and equals diameter of the described circle.
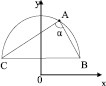
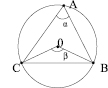
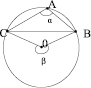
2. Let us prove that the inserted angle is two times smaller than the central one: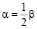 
(noth angles rest against the same arc – fig. 2).
Let us confirm that in case a) 2α = β. We have:
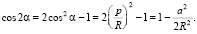
According to law of sines in triangle B0C
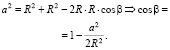(3)
But, on interval (0, p) equality of cosines of two angles results in equality of angles themselves.
3. For the given chord on the bigger and smaller arcs a point is taken (fig. 3).
Let us prove that view angles for the chord of these points are mutually supplemented up to p.
According to equality (1) cos α + cos β = 0. The left part is transformed to the form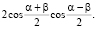 
Here cosine of half-difference does not equal zero, since α, β∈(0, p).
а) b)
Fig. 2. Illustration to proof of characteristics of the inserted angle
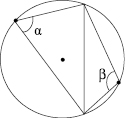
Fig. 3. Illustration to proof of statment on view angle of chord
Therefore,
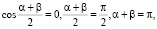
which is required.
Results and conclusion
The suggested project for students of profile mathematic classes “Other methods of ways to prove law of sines” drew certain cognitive interest among students, and many of them discovered different ways or methods to prove the named theorem.
Depending on type of proof terms “methods of proving” and “ways to prove” are used in methodical literature [4, 5]. Let us demonstrate, what is the difference between them.
If a proof of statement differs from anothoer proof of the same statement not by logical foundation, but sequence of conclusions, we should claim that the statement is proven via two different ways, in case one statement is distinguished from the other by its logical foundation, we speak of different methods of proving.
In conclusion we suggest the following problem for the reader: “What should length be for chord of radius R so that it is seen from the center of circle under the same angle as from points of smaller arc?”
Advice: use formulas (1) and (3).
Correct answer: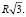 
New approaches towards organizing training-cognitive activity of students can be found in works [6, 7].