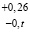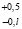Scientific journal

European Journal of Natural History

ISSN 2073-4972

ИФ РИНЦ = 0,301

Ships, drilling rigs, construction of bridges, development of gas and oil fields, acoustic equipment, as a technogenic sources of underwater noise, are significantly affect the noise level under water during the last years. In addition, energy is becoming popular in the water areas of various states, which, as electricity generation grows, increases noise load and, ultimately, affects the speed of changes in marine aqua ecosystems. The above circumstances, among others, actualize the problem of noise pollution of marine areas in the early XX century in the world.

Discussing the problem of intensification of noise pollution of marine aqua-ecosystems in the world, it should be noted that its solution should be based on methods of geo-ecological research and implemented on the basis of an assessment of the state of the ecosystems being studied [1].

Thus, the assessment of the safety level of marine aqua-ecosystems, as well as the ecological state of these objects as a whole, can be solved by analyzing and ranking the environmental and anthropogenic factors that are significant for the implementation of this assessment, as well as by using the well-known method of mathematical modeling for forecasting or scientific foresight of the possible state of marine aqua-ecosystems under investigation in the near future.

The safety of marine aqua-ecosystems in the case of noise pollution will be evaluated by interpreting the values of the calculated integrated indicator of ecosystem safety, the formula of which takes into account a number of empirical parameters and is presented in [2].

In turn, forecasting of the ecological state of the marine aqua-ecosystems under study can be carried out by extrapolation of the currently available numerical parameters. It is important to note that the prediction of the ecological status of any ecosystem should take into account the current characteristics of aquacombs (species diversity, the ratio of the number of species, etc.), since changes that occur in ecosystems necessarily affect them [1].

The extrapolation method assumes the construction based on the ranked data of the dynamics graphs of one or another parameter that takes into account the state of the aqua-ecosystem in the past and the current moments, and also the continuation of these graphs for a certain time interval depending on the tasks to be solved. Carrying out the extrapolation method, it should be remembered that in this case there is a timeless approximation, and the obtained predictive values of the investigated parameters will not take into account the dynamic oscillations or possible changes in the values of these parameters, proceeding from the assumption that the object will develop the same way as in the past and the present [3].

In general, extrapolation methods are quite widespread and are used in a number of studies, despite their inaccuracy and “smoothness” of the numerical solutions obtained. The basis of extrapolation-prediction methods is the study of empirical series. Empirical series can be numerical sets of the results of observations of a number of parameters obtained successively in time.

Other methods of processing empirical or chronological series of empirically obtained characteristics for solving the prediction problem of future numerical realizations are well-known and well described. In particular, in a number of research papers, methods of revealing the statistical connectivity of series members (Abbe’s criteria), methods for identifying “Markovism” (revealing a complex Markov chain), and others have been used and shown very interesting results [3].

In addition, empirical series of observations can also be fairly effectively investigated using the method of least squares. It is worth noting that the peculiarity of this method is that the prognosis for the whole period of anticipation will be calculated on the basis of the chosen function, despite the changes that are taking place. If the calculated values are close or coincide with the actual values of the original series, then it can be argued that it was possible to select a mathematical function corresponding to the dynamics of the original series.

Let us consider in more detail the determination of regression equations for estimating the changes in the parameters studied by the method of least squares described above. Characteristics and changes in parameters of the aqua-ecosystem for further forecasting will be recorded in the table 1 (Fig. 1). The data from the table can be represented in the form of n pairs of values (xj – the time meter, Yj – the value of the monitored parameter, where j = 1,...,n). Suppose that the linear regression function 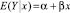adequately represents the situation of reducing environmental security. It is required to find estimates α and β, respectively A and B, and determining the regression line closest to the experimental points. If the “proximity” is measured by the sum of the squares of the differences between the observed values and those given by the constructed regression line, we arrive at the method of least squares (Fig. 1).

Based on the foregoing, an assessment of the level of safety can be characterized by an integrated indicator of ecosystem safety,

on condition |CPblvi| < |CPi| < |CPulvi|,

where Ci is the weighting coefficient of the i-th controlled parameter,

CPi – the value of the i-th controlled parameter,

CPulvi, CPblvi – the upper and lower limit values of the i-th controlled parameter,

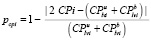– a dimensionless index of the safety of the i-th controlled parameter,

N – number of controlled parameters.

Fig. 1. Application of the least squares method to assess the ecological state of aquaecosystems

At the same time, if p = 0 – safety is 0% (that is, the safety level is zero – the state is catastrophic), if p = 1 (ideal) – without danger – safety is 100% – the state is ideal.

The proposed safety index, being integral in its essence, characterizes the state of the ecosystem under study, including a number of ranked parameters (Fig. 2).

An ecosystem is considered in a crisis situation and requires urgent intervention when it leaves at least one of the monitored parameters beyond the permissible limits.

As parameters of aqua-ecosystems under study, in connection with, for example, parameters can be:

– ecological (temperature, salinity, illuminance, species groups of aquabionts, ratio of species groups, indicators of population dynamics, etc.);

– Anthropogenic (levels of noise pollution, intensity and duration of noise pollution, etc.).

The investigated parameters can be obtained experimentally (measured), calculated theoretically (expert evaluation, theoretical modeling, etc.), by experimentally determining the parameters of the pollution zone / impact of the anthropogenic factor on the aqua-ecosystem under investigation.

The values of the investigated parameters in Table 2 (Fig. 2) are divided into two regions: the current data is the data obtained experimentally and theoretically up to the present moment of existence and the predicted values are values extrapolated from the known data for the further life of the aqua-ecosystem.

The graph of the regression equation for each parameter in the coordinate axes “parameter value-time” for parameters D1-D4 and R will have the following form (Fig. 3).

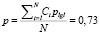
Fig. 2. An example of a security assessment of the ecosystem

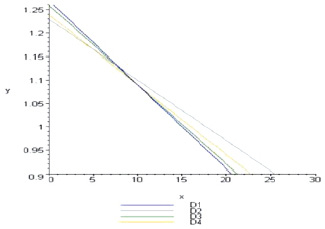
Fig. 3. Graph of the regression equation for D1–D4 (the density of the i – population)

Hence it is necessary to emphasize that the proposed approach to assessing the level of safety and the further ecological state of marine aqua ecosystems in connection with noise pollution allows not only to obtain a quantitative measure of the safety of the assessed object. Based on the calculations performed, it becomes possible to manage various, including negative scenarios, of the further state of marine aqua-ecosystems.

So, in a number of cases, an improvement in the situation is possible through the development of appropriate technical solutions, for example: the development of the foundation of wind turbine designs, bridges on piles driven into the seabed by hydraulic shock equipment; selection and design of noise-suppressing systems (dampers) based on thermoelastic alloys; air curtains; filled with air around the pile and so on.

In conclusion, it should be noted that the reduction in the level of underwater noise is the subject of highly specialized studies, since the differences between the conditions for a number of aqua-ecosystems are very significant, and this is important to consider.