The constituents of fractal objects are similar to the object itself. The object typically displays a structure, which is complex on some scales, and a metric dimension different from topological. A fractal pattern is typical of many geological objects and processes. The entire environment is often assumed to have fractal properties.
Fractal models are popular because they are simple and are briefly described. With a small number of parameters such models can adequately consider the properties of objects, reflect the integrity and hierarchy of a structural level and reveal hidden laws. In the humanitarian sphere, they allow to see simplicity in complexity, regularity in chaos, similarity in diversity, to connect many facts with a small number of hypotheses. In technical applications fractal models are used for data clustering and classifying and image processing. The potential of fractal models in natural sciences is far from exhausted.
The goal of the paper is to analyze the fractal properties of some natural objects, such as the lobar lines of ammonites, rock textures, river networks and varved clays, and to use them for solving geological problems. We seek to identify the type of ammonite on the dimension of the lobar line of its shell, to show that rock textures are fractals and that river networks and lake sedimentation are correlated to tectonics.
Lobar lines of ammonite shells
Ammonites are relatives of quids and octopuses and represent an extinct subclass of cephalopods named after the Old Egyptian god Amona. Ammonites came to exist in the Paleozoic, evolved completely in the Mesozoic and died off in the late Cretaceous Period. During this time span they were repeatedly born, died, spread over the ocean and evolved rapidly. In stratigraphy, this group of sea relics is used to estimate the relative age of sedimentary rocks, to subdivide rock sequences and to correlate geological units. It is most commonly used for the subdivision of the Jurassic (201-145 Ma) and Cretaceous (145 – 66 Ma) systems [10].
The soft body of a mollusk in a structurally complex ammonite shell occupies the last (living) chamber of the shell, while other chambers are filled with air. The gas regime of the chambers controls a siphon, a muscular strand which extends from the posterior end of the body through all chambers. The line of its attachment to the shell is called a suture or lobar line. As the lobar lines evolved, they became more complex presumably because the shell was getting more durable to be able to resist external factors such as water column pressure, water movement in near-shore zones, and to maintain the stable position of the soft mollusk body and the strand within the shell. The suture line could act as a marker during lit-par-lit shell formation.
Sedimentary rocks often contain shell fragments that can hardly be used to determine ammonite species. A lobar line can help in this case. Classifying ammonite with the help of a lobar line is like trying to reconstruct an object by analyzing its constituent. Curves that differ in shape can be compared in a simpler manner by analyzing their fractal dimensions.
The metric dimension of lobar lines was calculated in MATLAB computer mathematics package as a known cell dimension. The image region was split up into δ-sized cells and calculated the number of the cells N(δ) that cover the line plot. The cell dimension was doubled and the number of cells was re-calculated, etc. The data in the coordinates ln(δ), ln (N) were approximated by a straight line using the least-square method. The absolute value of the angular coefficient of the straight line was assumed to be the fractal dimension of the lobar line
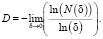 (1)
(1)
Fig. 1 shows the lobar lines of some ammonite species [5] (а-c) and their dimensions estimated using the algorithm described (d). The fractal dimensions of the lobar lines were D = 1.29 ± 0.02 for Spectoniceras elegantum, D = 1.34 ± 0.02 for Craspedodiscus borealis and D = 1.45 ± 0.02 for Deshayesites collevarus (Fig. 1 (d)).
It can be see from this example that different values of the fractal dimensions of the lobar line allow one to determine the type of ammonite.
Fractal Dimension of Rock Texture
The term “dimension stone” is applied to rocks used for the production of ornamental and facing materials, architectural structures and technical articles. This group includes igneous rocks such as granite, granite-gneiss, granodiorite, diorite, gabbronorite, gabbro-diabase, pyroxenite, peridotite, nepheline syenite, porphyrite and volcanic breccia; metamorphic rocks such as quartzite, quartzitic sandstone, marble, amphibolite, shungite shale and talc-chlorite schist; sedimentary rocks such as limestone, dolomite, calcareous tuff, limestone and gypsum. The characteristic features of dimension stone are decorative value, durability, unchangeable colour, mosaicity, wear resistance, water absorption, frost resistance and physico-mechanical properties. The aesthetic perception of dimension stone is attributed to its colour and ornament. The colours of the constituent minerals are responsible for the colour of dimension stone. Its ornament depends on the structures, textures and colours of rock constituents. Rock texture looks like a fractal image.
The fractal texture of a rock as a combination of contrasting mineral grains was studied using granite samples (Fig. 2) from the collection exhibited in the Museum of Precambrian Geology at the Institute of Geology, Karelian Research Center, Russian Academy of Sciences.
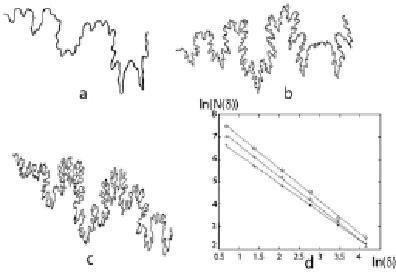
Fig. 1. Lobar lines of ammonites: а) Spectoniceras elegantum at a revolution height of 9 mm (*); b) Craspedodiscus borealls at a revolution height of 51 mm(о); c) Deshayesites collevarus at a revolution height of 60 mm (+); d) plots for estimation of cell dimensions
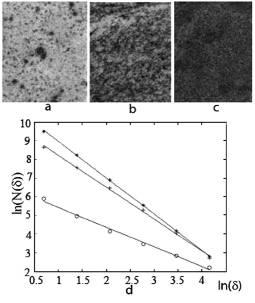
Fig. 2. Images of granites from Snezhny Bars (а), Shatkov Bor (b) and Lisya Guba (c) deposits, Karelia, and plots for calculation of their metric dimensions, “о”, “+” and “*” respectively

Fig. 3. Image of rapakivi granite (a) and the space distribution of the mineral grains of K-feldspar (b), quartz (c) and oligoclase (d)
Scanned images (а-c) were converted to a black-and-white format and inverted, assuming that the dark grains are the most intense. The fractal pattern of the textures of the images obtained was supported by the calculations shown in Figure 2d 1.07 ± 0.01 (a), 1.70 ± 0.01 (b), 1.94 ± 0.01 (c).
To estimate the fractal texture dimensions of polymict rocks, their images were subjected to pixel segmentation in colourspace by k-means clustering algorithm. The result of this procedure for rapakivi granite is shown in Fig. 3 [2].
The fractal dimensions of the K-feldspar, quartz and oligoclase distributions, respectively (r), estimated in this manner, were 1.71, 1.77 and 1.61.
The distributions obtained represent the real physical fractal components of rapakivi granite. It is known that fractal patterns affect the working capacity and cognitive abilities of a person [9]. By activating the brain stem structures and its regulatory mechanisms, they reduce fatigue, order
memory, increase resistance to stress. It is possible that the selection of rock textures with certain fractal properties can improve their aesthetic appeal.
Fractality of the Onega-Ladoga river network
River networks are traditional objects in fractal geometry. For a river network, as a system in which the energy of the ordered motion passes into other types, the fractal structure is advantageous and is realized due to the property of the system to choose a path with a minimum energy dissipation. The characteristics of the river network, calculated from the fractal model, are consistent with observations for the number of flows of a given order, their average length, catchment area and other parameters of river flow [1].
The rivers flow in topographic lows and are connected with crustal faults. Fractal dimension, reflecting the density and branching of the river network, may characterize the tectonics of the region. The verification of this assumption was carried out on the sections of the Onega-Ladoga hydrographic network (Fig.4a), selected by their proximity to the elements of the tectonic structure represented by the boundary of the Russian Plate of the East European Platform and the Fennoscandian Shield and the suture zone of the Svecofennian and Karelian blocks of the Fennoscandian Shield [8].
Fig. 4. The Onega-Ladoga river network with the elements of tectonic structure (a) and the sections of this network (b) chosen for analysis, the map of Fennoscandia [3] (c) and the plot (d) for the calculation fractal dimension of sections 1 and 4 (lines 1 and 2)
The boundary of the shield (Fig. 4, c), built by the hydrographic principle [6], is manifested by a stepwisw landform and the nature of the contact of Precambrian formations with a platform cover. Depressions, uplifts, tectonic zones, and horst-graben systems alternate along it. It generates seismic events, sets the starting level of the rise of Fennoscandia, causes the flooding of the coasts in Denmark and the Netherlands. The elevation of Fennoscandia and the deflection of the Russian Plate in the joint zone were responsible for the characteristics of the regional river network, forcing the rivers flow into this area from the north and south. The conjugation zone of the Karelian and Svecofenian geoblocks formed in the Late Archean as the boundary of the protocrust with the forming continental crust.
During geological time, there were manifestations of intrusive mantle magmatism here. Extensive evidence for neotectonics are found on Tulomozero Plain, stretching along the conjugation zone and on Valaam Island. Modern progress, as a rule, inherits ancient movements.
Fractal dimensions for the sections of the Onega-Ladoga river network (Fig.4b) were calculated (Table, Fig. 4, d).
Fractal dimension of the sections of the Onega-Ladoga river network
|
Number of section |
Fractal dimension |
Number of section |
Fractal dimension |
|
1 |
1,67 |
4 |
1,38 |
|
2 |
1,67 |
5 |
1,52 |
|
3 |
1,61 |
6 |
1,48 |
The values obtained for the fractal dimensions of the Onega-Ladoga river network sections confirm the characteristic pattern for the territory of Russia and the former USSR, the fractal dimensions of the river networks vary from 1,1 to 1,7 [7].
The river network sections, close to the elements of the tectonic framework, have increased fractal dimension values. With the removal from these elements, the fractal dimension of the network sections decreases. The proximity of the fractal dimensions of sections 1-3 and 4-6 is related to their position within the central and marginal parts of Fennoscandia’s border. The difference in these group of fractal dimensions is due to the remoteness of fragments 4-6 from the suture zone of the contact of the Svecofennian and Karelian geoblocks.
It is difficult to unequivocally interpret the influence of tectonics on river systems. On the one hand, its impact is associated with the feeding of rivers, their erosion work, changes in current direction, the morphology of the valleys and the river network density. On the other hand, rivers can arise without any contribution of tectonics, flowing out of swamps and lakes.
Calculations show that appreciable channel wanderings, invoked by erosion of rocks and sediments, are not characteristic of rivers flowing in rock massifs. Tectonics remains one of the main factors in the formation of the regional hydrographic network described. The continuing rise of Fennoscandia, the deflection and fragmentation of the Russian Plate contribute to the renovation of the former, the formation of new faults in the earth crust and the density of the river network. formation of new faults in the earth’s crust, the density of the river network.
Multifractal spectra of varved clay
Varved clay is a convenient material for the study of climatic changes and depositional environments. Varved clay deposits, formed annually in postglacial lakes, consist of light and dark laminae composed of sand supplied in summer and living organisms that died off in winter. The thickness of the laminae provides evidence for the velocity of sand supply and the freezing time of a water body. The multi-fractal parameters of varved clays were assumed to be sensitive to variations in sedimentation regime. This assumption was checked by analyzing varved clay samples from lakes Onega and Ladoga. Data on varved clay columns from lakes Onega (61о41’, 35o35’) and Ladoga (Heluli) are provided by S.A. Vyakhirev. The sedimentation process in them was described by numerical series represented by the ratio of a winter layer thickness to annual layer thickness (Fig. 5 a, b). The multi-fractal spectrum was calculated as a function of the Hausdorff dimensions f (α) from the singularities α [4]. The above calculations were carried out in the MATLAB computer mathematics system using the algorithm and program [4]. The multi-fractal varved clay spectra obtained are shown in Fig 5 c. These spectra display a typical bell shape with f (α) < 1.
It can be seen from Fig.5 that clay from Lake Onega is more regular than that from Lake Ladoga. Its narrow spectrum (curve 2) is close to mono-fractal, which is characteristic of the Brownian process. The spectrum of the clay column from Lake Ladoga (curve 1) is shifted and broadened. Its structure is determined by the singularity indices α in the range 1,025-1,30. The width of the spectrum is estimated from the perturbations of the sedimentation process.
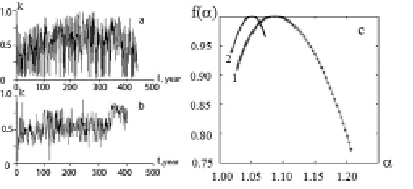
Fig. 5. Series of the ratio of the thickness of the summer puff to the thickness of the annual layer of sections of the varved clay of the Ladoga (a) and the Onega (b) lakes, their multifractal spectra (curves 1, 2), respectively (c)
In contrast to the Onega region, the Ladoga region shows a weak modern seismic activity.
Monitoring of seismic events on Lake Ladoga was conducted by monks of the Valaam Monastery in 1916-1927. In the epicentral zone weak earthquakes can cause hum, water boiling and luminous formations. These phenomena are often observed to the west and southwest from the Valaam island in a zone with underwater troughs, ridges of northwest stretch and the greatest water depths of 200-260 m. The effects observed seem to be associated with the ongoing discharge of fluids. Weak earthquakes could have been triggered by meteorological phenomena. Wind, waves and variations in the lake level invoke a seiche that generates micro-earthquakes. Such phenomena disturb the course of sedimentation and make this process irregular.
The influence of tectonics on sedimentation is demonstrated by changes in deep-sea formations triggered by shallow formations, and vice versa. The disturbance of stratification in banded clay sequences is especially noticeable in water reservoirs located near seismic dislocations. This disturbance makes it possible to estimate the years of an earthquake and the frequency of seismic events. The multi-fractal spectrum is capable of describing an irregular sedimentation pattern when the disturbance of stratification is poorly-defined.
Conclusion
The fractal nature of the objects discussed was proved by estimating their metric dimensions and multi-fractal characteristics. These characteristics of the objects are sensitive to the conditions of their formation and evolution.
The results obtained show that the lobar line of a shell is consistent with ammonite species, that dimension stone has a fractal texture and that the metric dimension of the river network and a multi-fractal sedimentation spectrum reflect the influence of the region’s tectonics.
The study demonstrates the efficiency of mathematical methods in natural sciences and the use of fractal models for setting and solving geological problems in particular.
The author expresses gratitude to Sergey Vyakhirev for the provided materials on varved clay columns.
This work was performed within the framework of the theme “3D Karelia lithosphere model based on geological and geophysical data”.

