Forests maintained the climate and hydrological regime of the Earth throughout its pre-anthropogenic history [10]. Currently, forests occupy about 52 % of the earth’s surface. These ecosystems play a large role in the world carbon budget and its dynamics. However, the forest area is decreasing on all continents [9]. This tendency is due to the huge scale of timber harvesting and fires, so the problem of reforestation and conservation of forest resources is becoming more urgent [11].
We studied reforestation in the Ural Mountains (Russia) for more than 20 years [3, 5-7, 12]. Quantitative data on the structure of indigenous forests, cuttings and secondary ecosystems of different ages were obtained. These data served as the basis for constructing mathematical models. The aim of the modeling was to forecasting of forest ecosystem dynamics as the basis for sustainable forest management. The cusp catastrophe was chosen as the basis for building models. The cusp catastrophe is one of the seven elementary catastrophes. In biological and behavioral sciences, the so-called cusp catastrophe model has been applied most frequently, as it is the simplest of the catastrophe models [2]. It is summed by the equation:
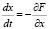 or
or 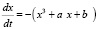 . (1)
. (1)
where F is the potential function that determines the energy characteristics of the system.
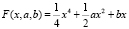 . (2)
. (2)
In the process of constructing a generalized model for the formation of vegetation after harvest, we described the basic concepts and equations of Catastrophe Theory. A quantitative mathematical model that takes into account the features of the region and habitat for the dynamics of the vegetation of the Urals was built. This model allows you to make quantitative predictions of real situations. The existence of alternative lines of the succession dynamics of forests in the habitat was formalized within the framework of catastrophe theory. Quantitative methods for assessing the sustainability of reforestation were proposed [1, 4, 8]. One of these methods is the construction of potential functions. Local and global stability of the forest ecosystem is determined by type of the potential functions (presence of minima and maxima). Special studies are devoted to the study of the effect of control parameters on the growth of woody plants [8]. As a result, the critical thickness of the soil is determined, at which the equality of the numbers of pine and birch on felling is observed. It was 27 cm for the southern taiga forests of the Middle Urals. Natural regeneration of pine predominates on shallow soils. Natural regeneration of birch dominates on powerful soils. As a result, various forests are formed on different soils. Calculations show a satisfactory agreement of theory and experimental data. It reflects the perspectives of the catastrophe theory for describing, analyzing and forecasting forest ecosystems dynamics, sustainability assessment and crises identification.
Methods of Catastrophe Theory allow to identify and predict crises in the development of forest ecosystems, which is very important for the management of bioresources. Modern models can be used to assess the desired trajectory and to estimate recovery rate or to forecasting possible scenarios. The methods of Catastrophe Theory are universal and can be used for all forests of the world and other ecosystems.

