Scientific journal

European Journal of Natural History

ISSN 2073-4972

ИФ РИНЦ = 0,301

Time lines is one of the most important object of statistic analysis. As scalar time line there is called a massive from N meanings of some dynamical system with constant step , где  The is examined a process of teaching at the higher education institution (university). As the xi we consider progress at the end of semester, Δt - time interval with the length of one semester, x₀ - progress by the results of Unified State Examination, N - the quantity of the educational semesters. Such statistic model we can build for the prognosis of progress at the end of one semester by the control points of calculation of progress during one semester. As there are no more than three control points at one semester, that the prognosis at the short interval should be with the big error. The calculations were leaded by the statistical facts of progress by the mathematics at the speciality "Applied mathematics" of Penza state university, where different sections of mathematics are taught during 10 semesters.

The treatment of statistic methods is based on the treatment of statistic model. At the statistic model the accent is underlined at the noise. For exit facts we have character distribution and character time correlations. The task of treatment consists in that thing to build a model such way, that is transform noise into a time line. At this way of building a model we can either demand the coincidence of several points of distribution, or use more complicated characteristics, such like the density of distribution. At the first stage we will require the coincidence of several points of distribution.

We know a time line x_i. At the each point we can create a "noise", this is a succession of uncorrelated and equally distributed accidental quantities ξ_i with the zero average. Let´s suggest that i element of the line x_i we can consider as some function, which depends on m of preceded elements x_i-1 , ...., x_i-m and accidental quantities ξ_i , ..., ξ_i-k:

 (1)

For the beginning one can limit oneself to the linear functions F, to the models of type

 (2)

Such model is called ARMA from the words autoregression (first sum) and sliding average (second sum). The coefficients ai, bj are found by the method of the least squares. This type of models is good for the prediction of next mean by the m previous. The real calculation of progress in maths in every next semester corresponded to the built model with little deviation and the error didn´t move over the limits of hundredth parts of the percent. While the studying of statistic models there were used following literature [1, 2, 3].

More exact prognosis of progress we can receive if we use the average mean of predictable quantity:

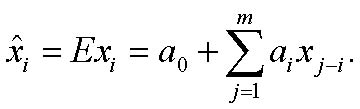
It´s suggested that previous means are known exactly. The noise is the compound part of linear models and linear prognoses can be done to the small number of steps forward.

The correlation (2) is a discrete analogue of compression of two signals: x(t) and ξ(t) with the finite functions a(t) and b(t):

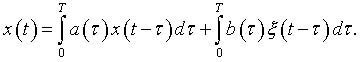
The interval [0, T] is considered as the interval of time of teaching of one section of mathematics of one semester length or, at the more general case, the whole period of studying maths at the higher education institution.

Using the transformation of Fourier 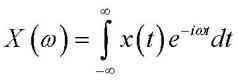, we get a compression:

At the result of transformation of Fourier we get an expression:

If we solve this equation concerning X(ω), we´ll receive

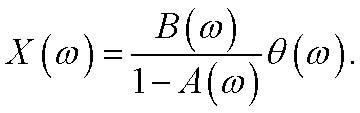 (3)

The selection of the functions a and b allows to transform the spectrum of noise θ(ω) such way, that it become analogous to the spectrum of analyzed signal.

Built linear model (2) is convenient that which it gives analytical results and its use doesn´t require a lot of mechanical time.

References

1. Box J., Jenkins G. The analysis of time lines. The prediction and direction. - M.: Peace,1974.
2. Katuan R.L., Rao A.R. Building of dynamical stochastic models by the experimental facts. - M.: Science, 1983.
3. Lung L. The identification of the systems. Theory for user. - M.: Physmathlit, 1991.