Nowadays in many countries of CIS and abroad a great attention is paid to study of effective resonance tunneling of electromagnetic waves through mediums with small-scale inhomogeneities [1-3]. It was proved that in most cases it is a non-reflective passage of waves in various mediums through different layers of an inhomogeneous medium. Particularly, such cases such cases were studied through layers of plasma inhomogeneity in lack of external magnetic field [3-4].
An analysis, undertaken for a number of situations (for example, works [2, 3]) showed us that it is possible to establish non-reflective tunneling of electromagnetic waves from vacuum into inhomogeneous layer regardless of dielectric penetration at the border of division. Here we should underline that analysis of exactly-solved models allows us to advance significantly in our understanding of spatial-time dynamics of electromagnetic fields in inhomogeneous dielectric structures with a strong spatial dispersion.
In this article we studied a linear single-dimension problem on resonance tunneling of an electromagnetic wave through a layer of gases in inhomogeneous medium at the example of ionosphere with small-scaled structures. We can outline that the simplest situations emerge in case of electromagnetic wave (or flow of particles) passing through a layer of ionosphere without external magnetic field or in case of spread of electromagnetic wave across homogeneous external magnetic field in magnet-active gas.
Main equations and solution of them
According to the above-mentioned, this work implements exactly-solved model of Helmholtz equation and also studied non-reflective resonant tunneling of transverse electromagnetic wave (or flow of particles) through a layer of inhomogeneous medium of gases with small-scale structures.
Thus, within the analysis of this work it studies standard relations between values of induction (B, H, E, D) in medium:
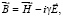
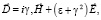
where γ is small parameter of inhomogeneity.
While studying a wave of flow of particles across homogeneous external magnetic field for wave field we use standard presentation of E(x, t) = F(x)exp(–iωt), where ω is wave frequency. In this case we receive for wave amplitude F(x) with Helmholtz equation [1]:
d2F / dx2 + k02 εef (x) F = 0, (1)
where axis x corresponds to direction of inhomogeneity, k0 = ω / c is vacuum wave number, εf(x) is effective dielectric penetration of gas. Thus, in case of wave spread in different layers of gas without external magnetic field we have εf(x) = 1 – [ωpe(x) / ω]2 where wpe(x) is electronic Langmuir frequency. In practice we see that during spread on unusual wave in magnet-active layer of gas across external magnetic field we can receive εf(x) ≡ N2(x) = ε⊥ – (εc2 / ε⊥). Here N is deflection index, εxx = εyy ≡ ε⊥ and εxy = – i εc – are components of tensor of dielectric gas penetration (for example, [4]). For the further analysis and simplification of problem we introduce variable ζ = k0 x and size-less wave vector Z(ζ) = c kx(x) / ω. Thus, exact solution of equation (1) is drawn similarly to [2, 3] as:
F(ζ) = F0 exp[i Ψ(ζ)] [1/z(ζ)] 1/2,
dΨ/dζ = z(x), F0 = const. (2)
Then, considering (1), (2) in order to establish exactness of solution, value of effective dielectric penetration εf(x) that is related to size-less wave vector z(ζ), obtains the following non-linear equation:
εf(ζ) = [z(ζ)]2 + (d2z/dζ2)/2z – 0.75(dz /dζ)2/z2. (3)
According to (3), in exact solution emerges a non-local relation between functions εf(ζ) and z(ζ), and it is a principal difference of it from classic solutions. Let us also introduce normed amplitude of wave |F / F0| ≡ A(ζ) = [1/z(ζ)] 1/2. In this case formula (3) can be drawn as an equation for wave amplitude with A(ζ) with cubic non-linear effect
d2A / dζ2 + εf(ζ) A – [1 / A(ζ)]3 = 0. (4)
We should outline that non-linear equation (4) for the given function of effective dielectric penetration εf(ζ) defines spatial profile of size-less amplitude of electromagnetic wave. Let us point out the following: in case of homogeneous layer of gas, when ?f(?) = const, solution to equation (4) for the fixed wave length, in other words, actual equation of non-linear oscillator without dissipation with ?f(?) > 0 describes both spread of electromagnetic wave or flow of particles in gas with constant amplitude A0 = 1/?f1/4 and also spatially-modulated wave set with parameter that defines values of variations Amin < A < Amax of amplitude А, besides, these variations can be rather large.
Further let us study non-reflective passage of transverse electromagnetic wave through layer of gas that occupies area 0 ? ? ? 3b, on the left (? = 0) and on the right (? = 3b) is borders vacuum. As the simplest analytic model that automatically provides at the border of gas layer ? = 0, ? = 3 b conditions for non-reflective seaming of fields that fall from the vacuum (? < 0) and distance to the right from gas layer (? > 3b) as electromagnetic waves, we use the following expression for size-less wave vector z(?) = 1 – m [1 – cos(g?)] where m-parameter of problem (0 < m < 0.5), g = 2p / b, b is parameter of gas layer thickness, further it is considered as b = 20. Included into this formula multiplier [1 – cos(g?)] provides for fulfilment of conditions of non-reflective seaming of fields of electromagnetic waves at borders gas-vacuum, specifically p(0) = p(b) = 1, dp / d? = 0 while ? = 0, ? = 3 b.
Let us introduce nominations g(?) = m g2 cos(g?), h(?) = 0.5 / p(?), q(?) = [m g sin(g?)]2. As a result, formula (3) for effective dielectric gas penetration is presented as:
?f(?) = [p(?)]2 – g(?) h(?) – 0.75 q(?) / [p?)]2. (5)
Numeral calculations show us that for m < 0.49 function ?f(x) < 1, and for m > 0.44 it is positive. In case m > 0.44, certain layers emerge in gas layer, in them ?f(x) is negative, and, according to classic concepts, it corresponds to gas opacity [4, 5].
A more generalized variant of model of gas inhomogeneities can be drawn, for example [5], as the following model of size-less wave vector p(?) = 1 – m f(?)[1 – cos (g?)], where f(?) is a limited function (generally-speaking, random), g = 2p / b is parameter of gas layer thickness. Multiplier [1 – cos(g?)], included into this function, provides for fulfilment of condition of non-reflective seaming of fields of electromagnetic waves at borders gas-vacuum, particularly p(0) = p(b) = 1, dp/d? = 0 при ? = 0, ? = b.
Research results and discussion
The received results can be studied as implementation of this function in dependence on parameters as well as calculation on the basis of computer programmes. Therefore, as an example we shall study the following variation of selecting function f(?):
f(?) = [1 + cos(2g?) – cos(3g?) –
– 0.5 cos(4g?) + 0.5 cos(5g?)], (6)
where m is free parameter of the problem, and condition f(0) = f(b) = 0 is fulfilled. Using expression (5) we shall calculate through formula (3) effective dielectric penetration ?f(?).
Let us study the variation of non-reflective interaction between electromagnetic wave with inhomogeneous gas layer with implementation of a more complicated function f(?), compared to expression (5), then
f(?) = 0.125 m [1 – 0.25 cos(g?) –
– 0.5 cos(2g?) – 1.25 cos(3g?) – cos(4g?) –
– 0.25 cos (5g?) – 0.5 cos(6g?) –
– 0.5 cos(7g?) – 0.25 cos(9g?)]. (7)
If we select these parameters, we receive variant of gases without external magnetic field, as well as certain graphs at the example of spatial profiles of dielectric penetration ?f(?) of wave number p(?) and other parameters, these graphs are presented below.
As we can see in fig. 1, profile of wave vector also includes layers of opacity in which ?(?) < 0. Let us outline that outside of layers of hybrid resonance there is correlation of maximum p(?).
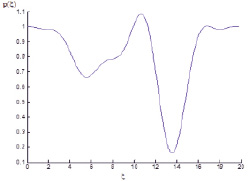
Fig. 1. Graph of dependence p(?)
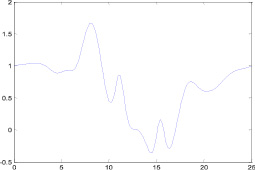
Fig. 2. Graph of dependence ?(?)
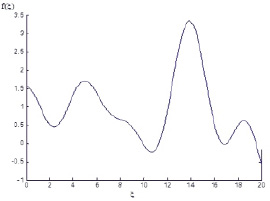
Fig. 3. Graph of dependence f(?)
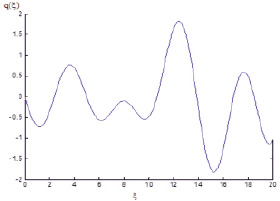
Fig. 4. Graph of dependence q(?)
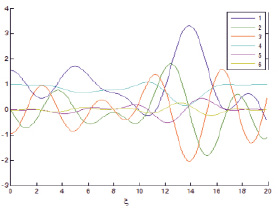
Fig. 5. Overall view of p(?), ?(?), f(?) q(?), totally 5 parameters
Since fig. 2 shows us that value ?(?) in inhomogeneous gas layer means that certain layers of opacity exist, in other words, spatil profiles of dielectric penetration ?(?), below zero it creates layers of opacity
As shown, in fig. 3, by changing function f(?) we can receive subwave structures for which non-reflective passage of electromagnetic waves through medium is realized.
As we can see in fig. 4, value q(?) is a dependence of effective dielectric penetration of different gases on wave number. Change in line of graph depends on parameter ?
As follows from the comparison in fig. 5, in overall view, decrease in parameters b and ? results in narrowing in area of gas layer opacity, value of main minimum p(?) becomes slightly larger, and value of maximum ?f(?) decreases several times.
Conclusion
The above-studied methodic of researching exact solutions to unidimensional problem through wave equation in terms of gas inhomogeneity can be of interest, for example, in regard to gas characteristics and electromagnetic wave, falling from vacuum as instrument of significant improvement in efficiency of absorption of electromagnetic radiation in the area of gas resonance. Obviously, the problem of resonance tunneling of electromagnetic waves through a layer or certain barrier draws interest in terms of various practical implementation. The studied exactly-solved models can reveal new features in dynamics of wave processes in inhomogeneous gas, especially non-linear processes in terms of strong inhomogeneity.
Thus, in this work at the foundation of exactly-solved models we have studied non-reflective interaction between electromagnetic waves and inhomogeneous small-scale structure of gas layer. The problem has a number of independent parameters, particularly thickness of inhomogeneous layer, depth of modulation of dielectric penetration, etc. By changing these parameters and using method of calculation through computer programmes we can receive graphs and a large number of completely – illuminated inhomogeneous layers with small-scale structures of gas layers.
Библиографическая ссылка
Gayurov Kh.Sh., Rahimova U. ON RESONANCE TUNNELING OF ELECTROMAGNETIC WAVES THROUGH THE INHOMOGENEOUS MEDIUM WITH SMALL-SCALE INHOMOGENEITY // European Journal of Natural History. 2019. № 4. С. 46-50;URL: https://world-science.ru/ru/article/view?id=33996 (дата обращения: 24.01.2026).

