Analysis of the work of domestic and foreign researchers in the field of mechanical activation, a bibliography which includes several thousand names [1], showed that modern advances in technology and milling technology is associated with the creation of new methods of organization of the process, the development of highly efficient low energy devices and metal [2, 3], constructed based on these methods, as well as the creation of the products obtained dispersion rational management systems. It was revealed that the introduction of hardware – technological systems of methods of physical mechanical activation using electromagnetic fields allows intensifying the classical technological scheme of production of products for various purposes, going to the one-step process of grinding, improve the quality and reduce the power consumption of finished products [4, 5]. A method of forming dispersing loads formed the basis of a new type of equipment – electromagnetic actuators (EMMA), can reduce energy consumption by tens of percent. It is proved that these apparatus can be regarded as power amplifiers [2]. To provide conditions for increasing energy dispersion process in EMMA is necessary to observe the principle of “necessity and sufficiency of energy supply” (or adherence to security and energy conditions), taking into account the kinetic energy and the patterns of the products grinding [6, 7].
The objective of the work: The object of research is the electromagnetic method of mechanical activation of materials for various purposes in magnetic fluidized layer ferrotel.
The material and methods of the investigation: Investigations were carried out on the basis of the dipole interaction model ferrotel in a magnetic field.
Results of research and their discussion
The electromagnetic mehanoaktivatore (EMMA) [8–10] the fracture energy is transferred to the material in the Acts of regulated energy-intensive multi-point contact between the grinding ferromagnetic elements. The force interaction ferro balls viewed as the interaction of dipoles in an external magnetic field undisturbed moments:
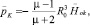(1)
where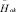 
– vector of the unperturbed magnetic field at the point of the space of the working volume of EMMA, which is the center k-s th grinding element with a radius R0.
The coordinates X, Y, Z dipole moment is equal to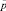 
:
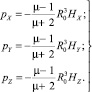(2)
Force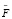 
acts on a dipole in a magnetic field determined system of equations:
;
;
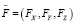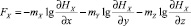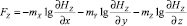; (3)
.
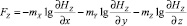where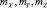 
– magnetic dipole charges; lg – shoulder dipole.
Taking into account the expressions for the magnetic charges:
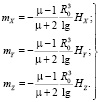(4)
Formulas for the determination of the forces Fr and Mν moments acting on the grinding elements in the working volume through EMMA layer activatable material:
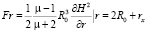; (5)
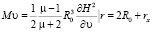. (6)
Numerical integration provides the following desired expression:
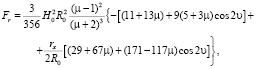(7)
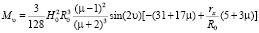. (8)
The work expended on product refinement of the original size to the final r1 grain size r2 static compression, determined expressions:
А = А1 + А2; (9)
;
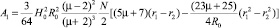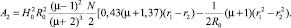
Where А1, А2 – the work of compression in the first and second periods of the formation of dispersing efforts; N – the number of grinding elements in the working volume of EMMA.
When the shock impact of the work is spent:
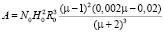, (10)
where N0 – the number of structural groups of ferroelementov.
In the process of mechanical activation energy change and technological properties of finely dispersed material, which are determined by the average level of WV and WΔV local energy densities achieved in the activation process. The stored energy is released to form a new surface ΔS. Parameter ΔS / V (ΔS – surface increase due to the grinding of the sample volume V) depends on the energy properties of the material, manifested in the surface energy values of WP, efficiency dispersion ηD, average WV (in the volume of the sample) and the local WΔV (in the centers of destruction) energy density at fracture:
ΔS/V ≈ (WV ηD) / WP
or
ΔS/V ≈ (WΔV ε V ηD) / WP. (11)
Assuming that the external input energy is concentrated in the process of deformation in structural defects, and in the act of dispersing converted into work disclosures structural grains, evaluation of specific energy consumption in the mechanoactivation largest possible local elastic energy density foci destruction (dispersing zones) and it can be determined by the formula:
WΔV = WV/εi = σ0ε0/2εi, (12)
where σ0, ε0 – tensile strength and deformation at the limit of strength;
εi – strain in the dispersion step.
Conclusion
When calculating recommended to use software package “ANSIS”, allowing to determine the electromagnetic field strength in a given system of contact points “ball – particle – ball” working volume EMMA any design modification [4] and to determine on the basis of the decision of problems of Solid State elasticity specific activation energy needed and sufficient to obtain stable predictable properties of activated materials for various purposes [12, 13].
Библиографическая ссылка
Bezzubceva M.M. THEORETICAL RESEARCHES OF WORKING PROCESS ELECTROMAGNETICALLY MECHANOACTIVATIONS OF THE PRODUCT IN THE MAGNETOLIQUEFIED LAYER FERROTEL // European Journal of Natural History. 2017. № 2. С. 10-12;URL: https://world-science.ru/ru/article/view?id=33712 (дата обращения: 03.04.2025).