There are two basic classes of developing systems (DS) (or evolutionary systems): 1) DS that are already have been created and have initial prehistory, 2) DS that are not have been created and have not initial prehistory. The second class is named originating DS [3]. Each of these classes divides, in turn, on three classes: Artificial DS (ADS) that are have been created by human beings and are functioning with their participation; Natural DS (NDS), in particular, the cell and cell associated objects [45]; and Joined DS (JDS): ADS and NDS as a whole [11]. Some examples of ADS are: industry, science, any educational center, including school, college, university, and education as a whole, art, health services, etc. The examples of NDS are the cell and cell associated objects, a separate plant, a separate organism, a population of animals, the biosphere, etc. We can consider the neosphere (in the sense by academician V.I. Vernadsky) as JDS that is the combination of two DS, one of which is human activity as ADS and another of which is the other part of our planet as NDS [11, p. 10]. The main elements of ADS are work places (WP). A work place is usually localized in the time and space aggregate of labor functions of the respective ware: material, energy, and information, which should be fulfilled by a respective specialist. The results of WP functioning in industry are various goods and services or products. The main characteristics or indices of the WP functioning are efficiency (the quantities of products produced per unit expenditure and per unit time). There are three important classes of WP: one that enters the DS from external environment or from other DS, the second reproduces or creates new more effective WP for the DS itself, and the third reproduces external goods with respect to DS. There are two branches of industry: one is called a subsystem A of DS in which DS creates new WP, and the second is called a subsystem B of DS in which DS creates or produces goods and services that are external with respect to DS. The distribution of WP by some control function y between the subsystems A and B is very important. The problem of this optimal distribution was investigated by V.M. Glushkov and V.V. Ivanov [9]. The main result is for small-term period of the time the desired y is minimally possible, but for large-term period of the time the desired y may differ from the minimally possible on the larger initial part of the time segment.
Modeling macroeconomic system academician V.M. Glushkov used a set of nonlinear integral Volterra type equations containing unknown functions not only in sub-integral expressions but in the lower limits of integrals. Introduction of function to the lower limits of integrals had important economic sense: this function was interpreted as a time boundary for the elimination of obsolete technologies for manufacturing system’s products. The proposed mathematical apparatus was applied later for modeling many other systems: ecological, biological, biophysical, medical, scientific enterprises, computing centers, populations, etc. Theoretical investigations and numerous applications have led to the creation of the theory of DS. Further development and generalization of DS Glushkov models [3, 5] (in particular, DS interaction with external environment, the latter being another DS) led to the creation by Glushkov V.M., Ivanov V.V. and S.K. Girlin of a new science that was named “Mathematics of Development” (on February 12, 2018, it was included in the “Register of new scientific directions”, № 0008). Within the framework of this science Girlin S.K. opened three fundamental laws of development [7, P. 77-79] (based on analysis of a number of theorems proven by Glushkov, Ivanov and Girlin). These laws can be set forth as follows.
First law of optimal development (“law of altruism”). If the size of planning time is small enough, the sought optimum of functional is arrived at the maximally possible (by virtue of limitations of task) use in the subsystem B of internal and external resources for implementation of basic function of the system.
Second law of optimal development (“law of reasonable egoism”). If the size of planning time is great enough, the sought optimum of functional is arrived at the substantial stakes of internal and external resources, using the subsystem of self-perfection on the internal necessities of the system on greater initial part of cutting-off of planning time and maximally possible use in the subsystem B of internal and external resources for implementation of basic function of the system at the end of it. This law was shown out of the theorems at general enough suppositions.
Third law of optimal development (“law of hierarchy of priorities”). If the size of planning time is great enough, the sought optimum of functional is arrived at the following priorities of allocation of internal and external resources between the subsystems of DS: first of all at the larger initial size of planning time the subsystem A1 (“science”) has priority (A1 is the subsystem, in which new technologies of system products creation functions of α and β kinds), then at the long time size has priority the subsystem of self-development A2 (the subsystem, in which new products of the first kind are produced, providing the fulfillment of the internal function of the system – its existence and development itself), and at the end of the planning time [t0, T] the subsystem B has priority, in which products of the second kind are produced, providing the fulfillment of the main system function to the system).
We`d like to notice that the law of “reasonable egoism” of the system can be considered as clarification of basic principle of communism: “to each – on necessities, from each – to abilities”.
Let us conduct a comparative analysis of models of V.M. Glushkov [9], models [3, 5] and a finite automat. A typical mathematical diagram of a finite automat is often used in modeling real processes. Following [2], let’s use the following definition of “a finite automat”. A finite automat is defined at discrete moments of time t0, t1, t2,... . If the unit of time period is defined as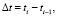 
then t = 0, 1, 2,... . A finite automat is characterized by finite sets of states z, input signals x and output signals y. At every moment of the automat time (except t0) an input signal x(t) is received in automat, under the influence of which the automat moves to a new state, in accordance with the transition function 
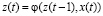and produces an output signal which is defined by the output function 
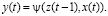If characteristics of zi, i = 1, 2, ... , are numbers, then the state z is regarded as the vector with coordinates z1, z2, ..., zn. In general, when zi are not numbers (for example, they are vectors, matrices, or objects of more complex nature), the state z is interpreted as “generalized” vector, and the features of zi are interpreted as its “coordinates”. The same can be said about the signals. The input signal appears as 
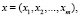and the output signal as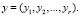 
An object of modeling can be seen as an evolutionary or a developing system (DS) [5, 9] if it contains at least two subsystems: subsystem A of self-improvement in which part of products of the first kind (which support the internal function of the modeled object by material, energy and information, i.e., its existence and development) create a new, more efficient (i.e., more productive) products of the first kind, and subsystem B in which another part of products of the first kind perform the main (external) function of the modeled object, i.e., the creation of some of the products of the second kind (executing the external function of the modeled object materially, energy and information-wise in interaction between the modeled object and its external environment). For example, in economic system products of the first kind are working places and products of the second kind are the products of a system created for an external “customer” (these products are goods and services that are external with respect to DS). The internal resources of DS will take only products of the first kind, which are sources of themselves and products of the second kind. Let’s call the external resources of DS the products of both the first and the second kind entering the DS from the external environment (however, some external resources become internal resources of the DS).
Using the above notations, the equations of the simplest two-product DS can be written as follows:
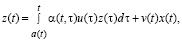
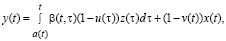
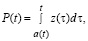
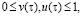
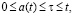
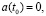
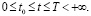
Here z(t) and y(t) are the rates of appearance in DS of the new products of respectively first and second kinds at the time t; x(t) – is the rate of entering of external resource in DS at the time instant t (x, z and y are assumed to be of one dimension); v(t)x(t) and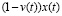 
– are the rates of entering in the subsystems A and B of the products of respectively first and second kinds at the time instant t,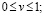 
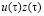and 
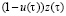– are the shares of z(τ) used for the manufacturing of z(t) (in subsystem A) and y(t) (in subsystem B) respectively, 
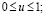a(t) – is a time boundary for liquidation of obsolete technologies for manufacturing first and second kinds products, which means that the product created before the threshold a(t), 
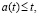is never used at time t, but the product created after the threshold a(t) is used entirely,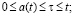 
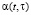and – are efficiency indexes of effectiveness of creation of the first (in the subsystem A) and the second (in the subsystem B) kind of new products at time t respectively, i.e., the number of units of z(t) and y(t) created in the unit of time starting from time t per one unit of u(τ)z(τ) and 
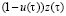respectively, 
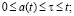t0 – is a starting point for modeling; for the segment [0, t0] we use prehistory of DS for which all the functions are given (their values will be noted by the same symbols but with the index “0”, e.g. 
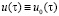and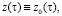 
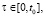
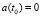; t0 and T is respectively the starting and ending point for DS modeling.
This two-product model can be easily generalized for multi-product and continuous models. External similarity between the two-product and the continuum models allows us to easily generalize the two-product model results concerning the existence and the uniqueness of a solution for two-product model [4, 7] to the continual and thereby multiproduct models.
If we put in the above system of equations and inequalities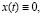 
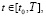we obtain as a special case of the DS model, originally proposed by academician V.M. Glushkov [8]. In this model [8] he assumed some predetermined nonzero initial prehistory (or initial condition) during the initial time interval [0, t0]. Let’s assume the given functions are such that the system of equations is completely determined. In this case, we get the problem of determining the dynamics of DS, in other words we need to solve the corresponding system of Volterra integral equations of the second kind with delay (typically nonlinear). From the theory of Volterra integral equations of the second kind it is well known that if on [t0, T] a free member is x(t) = 0, then the solution z(t) on [t0, T] of such an integral equation is zero. However, if we assume the function P(t) is positive and defined on the interval [t0, T], then, dividing the region 
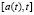of integration into sections 
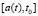and [t0, t],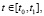 
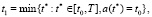it can take as a free member non-zero term in the first equation of the above system
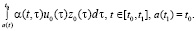
Clearly, the solution, which can be obtained, for example by means of the resolvent, will no longer be zero. Thus, in the case of setting positive function P(t) it is implicitly assumed that the non-zero state z(t) of the system is implicitly changed depending on some unknown input signal. If the initial prehistory is absent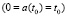 
or it is zero (z0(τ) = 0 or u0(τ) = 0,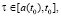 
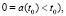then for the existence of a nonzero integral equation solution z(t) we need a non-trivial function v(t)x(t), which is interpreted as input signal of the system. These considerations have led to the introduction of the concept of “originating developing system” [3].
Following [3], let’s call the originating DS such a DS, for which the initial prehistory (or initial conditions) is absent (in this case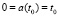 
, 
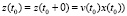or where initial conditions are equal zero: z0(τ) = 0 or u0(τ) = 0,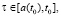 
.
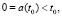
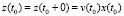Interestingly, if the function a(t) is increasing strictly on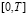 
(this case can be interpreted as a permanent removal of obsolete technologies as a result of scientific and technical progress), and continuous functions P(t), x(t) are set on 
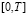then the solution z(t), 
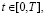depends on the resolvent of the first integral equation of the above system, functions P(t), x(t), and does not depend on the initial condition z(0) [4, p. 108-112]. Note that the introduction of a non-zero free terms v(t)x(t) and 
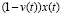into the equations allowed us to study not only a new class of the originating developing systems, but also to look for solutions in a more general class of piecewise continuous functions z(t) and y(t) (in the Glushkov equations z(t) and y(t) are sought in the class of continuous functions).
In addition, introduction of a piecewise continuous function v(t),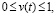 
allowed to expand the ability to manage the DS dynamics: in particular, in solving problems of optimal control we can use not only the controlling piecewise continuous function u(t), 
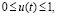which distributes internal resources between subsystems of the system to ensure the very existence and development of the system, but also the controlling piecewise continuous function v(t), 
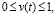which distributes external resources between the subsystems of the system to ensure the existence and development of the system and the execution of the main functions of the system.
Conclusions
A comparative analysis of models of developing systems and a finite automat is conducted. It is shown that a developing system originally introduced by Glushkov is not an open dynamical system (for example, for the case of missing or zero initial prehistory). To resolve this substantial deficiency Ivanov V.V. [10] attempted to introduce the input influence in the notations of the present work function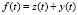 
(which can be interpreted as the predetermined potential ability of the system to produce products of the first and second kind in the time unit). However, from our point of view it is much more convenient (especially for the purpose of managing the dynamics of DS) to introduce as inputs functions x(t) and v(t). In addition, the introduction of such functions allows to formulate and solve new mathematical problems that are highly important for practical use (e.g., a problem of cooperative interaction of developing systems [1], a problem of modeling optimal import substitution in economic system [9]).
The authors are grateful to Oleg Polischuk for language assistance and useful remarks.