We study convex sets M ≤ Sⁿ, where Sn is an n-dimensional sphere.

The set M ≤ Sⁿ is strictly convex [1] when it doesn’t contain diametrically opposite points of the sphere and with any pair of points it contains a small arc of a great or a certain (definable) circle.

We prove the following

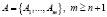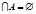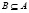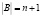Theorem. Let there exists the set of closed strictly convex sets such that 1) , 2) for all sets s.t. and 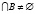and for all natural numbers k satisfying conditions 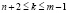minimal number of subsets 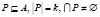is equal to 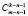, so maximal number of subsets A, containing k elements with the empty intersection is .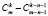