§1. Problem statement
Let´s consider the differential operator of the fourth order with the summable potential, which is given by the differential equation
(1)
and boundary conditions of a following kind:
(2)
(3)
where λ is the spectral parameter, function q(x) is called as potential.
We will assume that the potential is a summable function on a segment [0; π]:
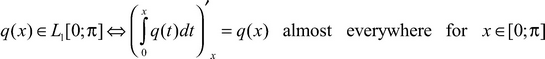(4)
Differential operators of a kind (1)-(2) with a condition (4) have started to be studied recently. Fundamental work [1] for the differential operator of the second order has appeared in the 2000 year. In it for the differential operator of the second order with summable potential it is received asymptotics of any order for solutions of the differential equation and asymptotics of eigenvalues of any order. In work as the [2] method which is distinct from a method of work [1], the differential operator of the fourth order in case of summable potential was studied. In the monograph [3] method of the work [2] is generalised on the differential operator of the 2n-th (n = 2, 3, 4, ...) order, on the functional-differential operators of the second and fourth order, and on the differential operators with discontinuous weight function.
The condition (3) provides so-called «effect of splitting» multiple in the main eigenvalues of the considered differential operator which in work [4] was considered by the author for the differential operator of the second order with discontinuous potential. As far as it is known to the author, for a case of differential operators of the fourth and higher order the given effect was not studied even for a case of the smooth potential.
§2. Asymptotics of the solutions of the differential equation (1) at 
For studying of asymptotics of eigenvalues of the boundary problems connected with the differential operator (1)-(3), it is necessary to know of the asymptotics of the solutions differential equation (1).
Let 
- some fixed branch of a root chosen by a condition 
. Let wk are the roots of the fourth degree from unit, that is
Numbers ωk are on the unit circle and divide it into four equal parts.
In the work [2] we have proved the following theorem.
Theorem 1. The general solution of the differential equation (1) has the following expression:
(5)
where 
- arbitrary constants, 
- linearly independent solutions of the differential equation (1), and for are valid following asymptotic decomposition:
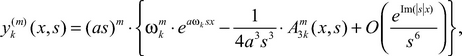
(6)
Following formulas are thus true:
(7)
An idea of decomposition of a kind (6)-(7) we have stated in the chapter 5 of the monograph [3].
The fundamental system of solutions 
for the differential equation (1) is a generalization of the fundamental system of solutions for the differential operator of the second order, which is consisting from Josta´s functions.
§3. Studying of boundary conditions (2)
From boundary conditions (2) by means of formulas (5)-(7) it is received:
(8)
(9)
The system of the equations (8)-(9) represents the system of two equations with four unknown variables which owing to conditions 
has the unique solution
(10)
Substituting formulas (10) and (5)-(6) in the remained two boundary conditions from (2), we will receive system from two equations with two unknown variables which has nonzero solutions in that and only that case when the determinant of this system is equal to zero.
Therefore the following statement is true.
Theorem 2. The equation on the eigenvalues of differential operator (1)-(2)-(3) has the following expression:
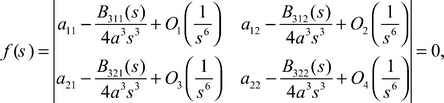(11)
in which the following designations are entered:
(12)
In formulas (11)-(12) we have entered a following designation:
Expanding the determinant from (11) on columns for the sum of determinants, using properties of determinants, we receive:
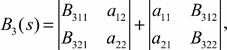(13)
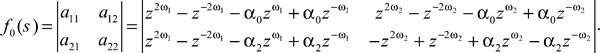(14)
The equation «in the main approach» on the eigenvalues for the equation (13)-(14) is the equation
(15)
Expanding the determinant from (14)-(15) more detaily, it is possible to understand that the indicator diagram (that is the convex polygon constructed on powers of exponents, entering into the equation (15), see [3]), is a square, with tops A(2; 2), B(-2; 2), C(-2; -2), D(2; -2), and on each of the sides of this square there are two points. We will tell, on the side AB there are points Н(-1; 2) and Е(1; 2). Eigenvalues of the boundary problem (1)-(3) considered by us there are in four sectors of the infinitesimal angles which bisectors are middle perpendiculars to the sides of square ABCD.
Theorem 3. The equation on eigenvalues «in the main » of the boundary problem (1)-(2)-(3) for the side AB of a square ABCD has the following appearance:
(16)
Substituting the condition (4) in the equation (16) we can divide on 
and by replacement 
reduce the equation (16) to the equation of the fourth degree 
, which has a simple root X4 = -1 and a third-tuple root 
.
Let´s consider the sector connected with segment АВ. We will leave in the equation (12) only the main terms on growth exponents.
Theorem 4. The equation on eigenvalues of the boundary problem (1)-(2)-(3) for the side BEHA of a square ABCD has the following appearance:
(17)
and it is possible to write out g3(s) in an explicit form, considering formulas (11)-(13).
§4. Asymptotics of eigenvalues of the differential operator (1)-(3)
Let´s consider at first a case simple «in the main» eigenvalue X4 = -1. In this case we have:
- the basic approach for the side BEHA. Therefore the methods stated in the fifth chapter of the monograph [3], prove the following theorem.
Theorem 5. Asymptotics of eigenvalues of the boundary problem (1)-(2)-(3) in sector of segment BEHA of the indicator diagram has the following appearance:
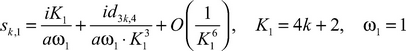(18)
and the coefficient 
is equal
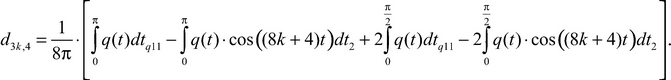(19)
Asymptotics of the roots of the equation (17), considering formulas (16), (12)‒(14), we will search by the method consecutive approaches of Horn. We will substitute the formula (18) in the equation (17) and we will equate coefficients by the same degrees K1. We will come to a conclusion that the formula (19) is true.
Let´s consider now a case of a third-tuple root .
Theorem 6. Asymptotics of eigenvalues of the boundary problem (1)-(2)-(3) in sector of segment BEHA of the indicator diagram has the following kind:
(20)
and the factor 
is equal
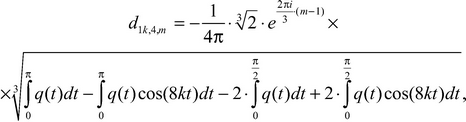(21)
where m = 1, 2, 3, that is we see that there was «splitting» multiple (third-tuple) «in the main» a root on three simple series of eigenvalues of the boundary problem (1)-(2)-(3),
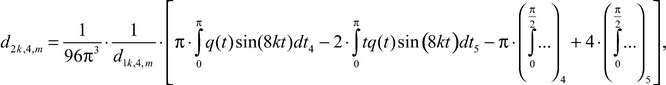(22)
under the condition 
, (and, if 
, then 
, and all eigenvalues of the boundary problem (1)-(2)-(3) are found in an explicit form under the formula
(23)
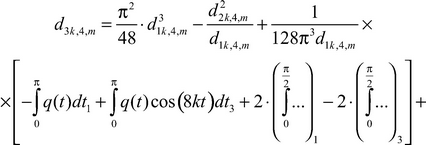
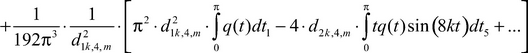(24)
The remark. If instead of the differential equation (1) we will consider the equation
with boundary conditions (2)‒(3) (exactly such differential equation the author has considered in the work [2]), then the considered formulas (18) and (20) will be rewriten in a kind
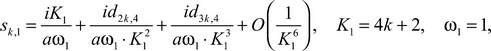
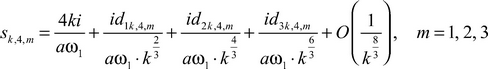
(that is there is «splitting» on fractional degrees).
If we will renumber the sectors connected with sides AB, BC, CD, DA of the square ABCD by numbers 1, 2, 3, 4 then the following theorem is fair. (Its proof is similar to the proof of theorems 5 and 6).
Theorem 7.
(25)
The formulas similar to formulas (18)-(24), for boundary problems of type (1)-(2)-(3), can be received and for cases of differential operators of the sixth and eighth orders.
Formulas (18)-(24) it is enough for calculation of the first regularized trace of the differential operator (1)-(2)-(3).
References
-
Vinokurov V.A., Sadovnichy V.A. Asymptotics of any order of eigenvalues and eigtnfunctions of boundary problem of Sturm-Liouville on a segment with summable potential. - Izvestiya RAS. Seriya: Mathematics. - 2000. - B. 64, №4. - P. 47-108.
-
Mitrokhin S.I. Asymptotics of eigenvalues of the differential operator of the fourth order with summable coefficients. - Vestnik Moscovskogo Universiteta. Seriya 1, Mathematis and Mechanic. - 2009. - №3. - P. 14-17.
-
Mitrokhin S.I. Spectral theory of operators: smooth, discontinuous, summable coefficients. - М.: INTUIT, 2009. - 364 p.
-
Mitrokhin S.I. About «splitting» multiple in the main of eigenvalues of multipoints boundary problems. - Izvestiya VUZOV. Seriya: Mathematics. - 1997. - №3(418). - P. 38-43.