Lately there has been a high demand for researches of wave resonant tunneling through micro-scale inhomogeneities effectiveness. In particular for reflectionless waves (of different nature) passage through significantly thick layers of inhomogeneous environment [1-4].
There are plenty of approaches but the most constructive one is using exactly soluble models of inhomogeneous environment waves’ interactions. Using these models makes it possible to examine wave processes in cases when approximate methods are obsolete or useful, because of inhomogeneities of high amplitudes. For example, waves’ reflectionless tunneling through plasm is important for radiation yield from sources that are in dense plasma in astrophysics, it is also interesting for powerful electromagnetic radiation absorption effectiveness intensification, when plasma is heated to thermonuclear temperatures as the result of wave penetration to dense plasma, and also for gases [5].
In this work we examined accurate solutions for Helmholtz equation, that describes reflectionless tunneling of electromagnetic wave through a wide inhomogeneous gas layer of ionosphere with micro-scale structures of its high-density amplitude.
Analysis of exactly soluble models of electromagnetic waves and inhomogeneous environments interactions appeals for many applications, for example, development of radiotransparent materials for aerials, searching for effective electromagnetic signal transmission through dense plasma layer [6].
This work presents research results based on linear reflectionless drop of electromagnetic wave to gas layer of final thickness containing micro-scale inhomogeneities of gas density (at scale of vacuum wave length).
Analysis of waves with inhomogeneous environments interactions was carried out based on Helmholtz equation for monochromatic electromagnetic wave field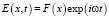 
which is written by
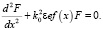(1)
Here k0 =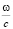 
is a vacuum wave number, εef(x) is effective dielectric permittivity of inhomogeneous environment.
In case of gases it is determined with directional concentration distribution and without external magnetic field for electron modes we have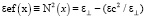 
, where N is a refraction index, 
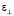and εc are components of dielectric tensor at upper hybrid resonance frequencies.
Analogously to [2, 3] the accurate solution to equation (1) is defined with formula
,
,
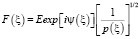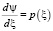here E = const [2, 3], defined with wave power flow. Wave number is defined with formula
.
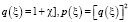In that case dielectric permittivity of gases is determined with formula
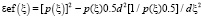
with parameters χ, b, a = 2πn.
For the dimensionless wave amplitude we have formula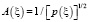 
. In inhomogeneous layer 0 ≤ ξ ≤ b it follows that p2 > 0 is constraint. As the most simple analytical model, which at the borders of gas layer ξ = 0, ξ = 3b automatically provides conditions of reflectionless cross-linking of incident electromagnetic wave from vacuum (ξ < 0) and electromagnetic wave outgoing to the right from plasma layer (ξ > 3b), we use the following formula for dimensionless vector p(
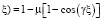, where μ task option (0 < μ < 0.5), γ = 2π/b gas layer density option, below it is determined as b = 20.
For example, let’s examine the following function selection f(ξ).
f(ξ) = [1 + cos(2γξ) – cos(3γξ) – 0.5 cos(4γξ) + 0.5cos(5γξ)], (2)
Reflectionless interaction of electromagnetic wave and inhomogeneous gas layer when choosing more complicated function than (2) formula,
f(ξ) = 0.125μ[1 – 0.25cos(γξ) – 0.5cos(2γξ) - 1.25cos(3γξ) – cos(4γξ) – 0.25cos(5γξ) –
– 0.5cos(6γξ) – 0.5cos(7γξ) – 0.25(9γξ)],
Let’s introduce the following notations: а1 = –0.25, а2 = –0.4, а3 = 0.71, а4 = 0.91, γ1 = 3.11γ, γ2 = 2.77γ, γ3 = 1.67γ, γ4 = 4.17γ, and some functions are as follows
, 
,
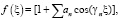
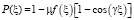
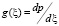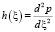it will allow to rewrite the equation more convenient and consider far more summands in it.
g(ξ) = –μγf(ξ) sin(γξ) + μ[1 – cos(γξ)]Σanγnsin(γnξ),
h(x) = 2 mg sin(gx)Sangn sin (gnx) – mg2 f(x) cos(gx) + m[1 – cos (gx)]S angn2cos (gnx)],
g = 2p / b, where b = 25
First of all, when m = 0.18 and computing results ef(x) an effective dielectrical plasma permittivity will be
ef(x) = [p(x)]2 + [h(x)/ 2p(x)] – 0.75 [g(x) / p(x)]2
f(x) = 2,599, g(x) = 0,0959,
h(x) = –0,0462, p(x) = 1.
Choosing these parameters we obtain option for gases without external magnetic field, and also dielectric permittivity ef(x) spatial profile diagram, character p(x) and other parameters.
As we see at the picture 1, wave vector profile includes opacity layers, where ε(ξ) < 0.
Therefore, in this work we have examined reflectionless electromagnetic waves’ interaction with inhomogeneous micro-scale structures of gas layers using exactly soluble equations. There are some independent parameters, particularly, inhomogeneous layer thickness, modulation depth of dielectrical permittivity etc. Parameters changing makes it possible to obtain a lot of fully-clarified inhomogeneous layers with micro-scale gas layer structures.
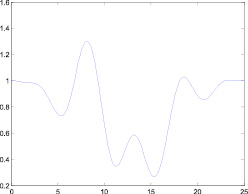
Fig. 1. Dependency diagram p(x)
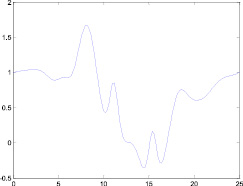
Fig. 2. Dependency diagram ε(ξ)
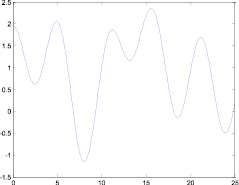
Fig. 3. Dependency diagram f(ξ)
It’s important that inhomogeneity could be represented as arbitrary number of different layers, with a number of independent parameters stratification.