The process of grinding solids represents a major scientific and technical problem caused by the lack of a generalized theory, thoroughly explaining the process and giving a precise mathematical apparatus for designing grinding equipment, meet the requirements of production in terms of efficiency and selectivity [1]. In this regard, the products of different grinding high energy consumption. As a result of comprehensive research revealed a mismatch between technological and physically-based energy consumption of the mills at all stages of dispersion and mechanical activation. To solve this pressing problem requires a qualitative shift to the design of the grinding device, based on the principles of providing maximum approximation of the energy consumed by the device from the network to the physical-based energy, given the hardening of particles with decreasing size in the milling process [2]. On the basis of theoretical and experimental studies, adaptive systems, providing a balanced and controlled energy effect on the particles of the comminuted product are solenoid mechanoactivation (EMMA). The study of regularities of formation of shock-abrasive loads in magnetic liquefied layer of electromagnetic mechanoactivation is an urgent problem in the development of energy efficient mechanoactivation.
The objective of the work: The object of research is the patterns of formation of shock-abrasive loads in magnetic liquefied layer of electromagnetic mechanoactivation.
The material and methods of the investigation: Used experimental and statistical research methods.
Results of research and their discussion
Grinding process in grinder-mechanoactivated is simultaneously both random and static in nature [3]. By analogy with drum mills in a disk mechanoactivated randomness manifests itself in the collision of particles with the grinding elements, and the static – that the process involved an infinite number of particles and, thus, they are very diverse in their physical and mechanical properties. It is also assumed that the grain particles have a spherical shape.
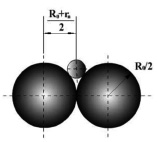
Fig. 1. Area of collision of the balls
Thus, the probable number of particles in the impact area of the grinding balls:
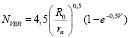, (1)
where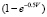 
– a function of the probability of finding the particles in an impact zone;
V – share fill grinder-mechanoactivated material.
In the process some particles are pressed into the surface of the grinding elements, the other pulled from the surface by their relative motion. Therefore, making the assumption that the grain size is at equilibrium these two processes, the formula for the probable number that came under attack, has the form:
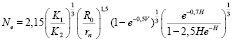, (2)
where –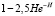 
the probability of detachment of particles pressed in contact with a particle in another bowl (this function has a definite view): very large and very small N the probability of separation is very high;at intermediate hardness, the probability will be minimal (in Н = 1 the function has a minimum value 0,08).
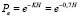– the probability function of the indentor particles in the grinding element at impact; Н – the ratio of hardness of the particle (coefficient k = 0,7 is determined from the condition that Н = 1, function Re = 0,5 equiprobable).
From the equation it is seen that the number of particles Ne is relatively insensitive to changes in probability coefficients k1/k2, for this reason, they can be neglected in further calculations.
Based on the foregoing, L.F. Bilenko displays the formula [2], allowing to determine the speed of the grind product in a drum mill with ball loading (the rate of grinding proportionally the number of particles in the impact zone, the probability of fragmentation particles in the zone at least once, the factor limiting the freedom of movement of the grinding elements, when the material in the mill lot):
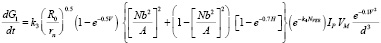, (3)
where G1 – the amount of product per stroke, which can be presented to the newly formed surface;
(Nb2/A)2 – the probability of the opposite event;
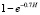– the probability of introducing particles to the grinding element at impact.
The product of these last two functions gives the probability that the particle will be sandwiched between clean surfaces and will not stick to the grinding element (i.e. for soft particles).
Function (Nb2/A)2 + 1 – (Nb2/A)2 (1 – e–0,7H) determines the probability of holding a single particle between any type of surfaces (the probability of occurrence of one of two incompatible events is the sum of their probabilities). And since the hardness of the steel grinding elements, a lot more the hardness of the grains, N >> 1, then the function will take the value equal to one.
Function: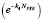 
– determines the probability of crushing particles in the impact zone (and, if you increase the number of particles in the cell it is reduced).
The expression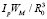 
– determines the number of grinding elements of the disposer – mechanoactivated (where Ip – the proportion of filling of the chamber the grinding elements, and WM – the volume of the chamber chopper).
Function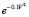 
there is a possibility of restriction of freedom of movement of the grinding elements in the presence of the material.
Given these provisions, the formula (3) with regard to the material component of the feed can be simplified:
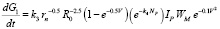. (4)
Making the assumption that each hit generates the same increase of surface, the formula (3) describing the amount of milled grain product can be brought to mind, characterizing the increase of the surface S1.
If S1 = kG1 (или dS1 = kdG1), the increase in surface occurring in a single blow:
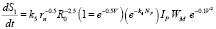. (5)
High-speed shredding will be observed for the solid material when filling the space between the grinding elements is approximately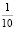 
, for soft-about half. Moreover, with decreasing particle size, the probability of their falling into the grinding zone will be reduced, and therefore, is preferred grinding larger particles.
The fundamental theory underlying the mathematical modeling of the magnitude of the force of contact between the ferromagnetic elements in the phases of working process (formation, destruction of structure groups of ferroaluminum, the formation of “layer sliding”) based on the development of the dipole model Maxwell [4–6]. Examining and setting the quantitative parameters of the energy process occurring with one structural group of Ferrochrom, and multiplying the result by the number of structural groups in the amount of handling of the product, you can determine the energy of the working process of the formation of dispersive loads in EMMA. When calculating the number of chains of ferromagnetic grinding elements is determined by the expression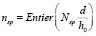 
(here Nsp – the number of grinding elements spherical shape in the working volume EMMA; d – the diameter of the grinding element; h0 – distance from stator to rotor). When developing the linear theory makes the following assumptions: power Fr and moments Mv, acting on the magnetized grinding element in the working volume EMMA, determined on the basis of the dipole models Maxwell’s; the diameters of the grinding elements is less than the width of the working volume (d << h0) and a lot more particles of the processed material (d >> rf); structural groups of grinding elements until the moment of their destruction when the critical angle of the structural groups of Ferrochrom vcr the transition in the phase of formation “layer slip” is not interact.
Taking into account the original size of the particles rf, power Fr and moments Mv, acting on the grinding element of radius R0 in a magnetic field with a strength Н in the working volume EMMA, determined by the equalities [6, 7]:
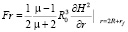, (6)
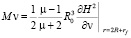. (7)
Critical angle vcr, in which the attraction of the balls is replaced by their repulsion, is defined by the formula:
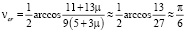. (8)
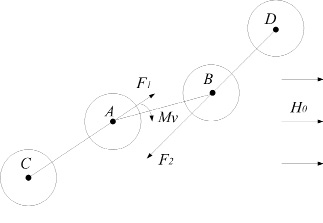
Fig. 2. Deformation of structural groups of grinding elements in EMMA
The equilibrium structural group
In areas of AB, DF, etc. the tilt changes from 0 до vcr. Therefore, in these areas the force of attraction of the balls also changes. For simplicity, the compressive forces in these areas takes some average force acting on these sites and corresponding to the angle value vcr:
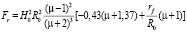. (9)
Corresponding to this force, work is defined by the formula:
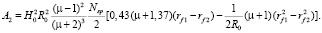(10)
Thus, the work expended on the crushed product from the initial grain size rf1 to a final size rf2 static grip between the balls equal to: Acmp = A1 + A2. The destruction of the structural groups of Ferrochrom all spent working on changing the angle v to kinetic energy, which is consumed on impact of destruction of the product. The rotation of the object AB, DF, etc. at the expense attached to them moment Mv, which is calculated according to the formula (4). This formula can be neglected with respect to rf/R0 compared to the unit:
M(ν) = F(ν) 2 R0 sin ν – Mν(ν). (11)
The work done to turn Nob / 2 objects of type AV on the angle from 0 to π/6 defined by the equality:
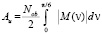. (12)
The final formula for the calculation of work impact fracture of the product is as follows:
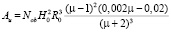. (13)
In the process of mA change energy and technological properties of finely dispersed material, which are determined by the level of the average WV and local WΔV energy density achieved in the activation process. The stored energy is released with the formation of new surface ΔS. Option ΔS/V (ΔS – the growth surface by grinding the sample volume V) depends on the energy properties of the material, manifested in the values of the surface energy WP, Efficiency dispersion ηD, average WV (in the sample) and local WΔV (in the centers of destruction) the energy density at failure:
ΔS/V ≈(WV ηD) / WP or
ΔS/V ≈ (WΔV ε V ηD) / WP. (14)
Assuming that the externally supplied energy is concentrated in the deformation process the structural defects, and in the act of dispersion is converted to erection work structural grains, the evaluation of specific energy consumption for the mechanical activation of the value of local elastic energy density in the foci of destruction (zones of dispersion) and can be defined by the formula:
WΔV = WV/εi = σ0 ε0/2εi, (15)
where σ0, ε0 – tensile strength and strain at tensile strength; εi – deformation at the stage of dispersion.
The calculation used the software package “АNSYS” to determine the intensity of an electromagnetic field in a given system contact points of the “ball – particle – ball” working volume EMMA any structural modification and determine on the basis of the decision of problems of elastic solids the specific activation energy necessary and sufficient for obtaining stable and predictable properties of activated materials for various purposes [7–9].
Conclusion
Physico-mathematical modeling of the process of the formation of dispersive shock-abrasive loads between the grinding ferroaluminum in structural groups through the layer of the processed material and analysis of the models improves energy efficiency design EMMA for various purposes.