AMS Subject Classification: 11 Number theory, 11G Arithmetic algebraic geometry (11G99), 11P Additive number theory; partitions (11P99).
Introduction. Beal’s Conjecture as generalized Fermat’s Last Theorem (formulation of the problem)
Beal’s Conjecture [1] deals with arbitrary positive whole powers of natural numbers except the second combined in one equation similar to the well-known equation of Fermat’s Last Theorem. The Beal proposition can be solved by the ancient Greek arithmetic geometry methods applied successfully as well to the Fermat problem [2]. Among all well-known mathematics conjectures Beal’s Conjecture is occupying a peculiar place being a generalization of Fermat’s Last Theorem [1]. However the generalization in [1] concerns only the formal record of this conjecture and does not summarize the methods of proving Fermat’s Last Theorem. On the contrary, the Beal conjecture comes to the Fermat problem considered as an arithmetic geometry problem with elements of combinatorics and has easy simple solution obtained by additive number theory methods apparently available to ancient mathematicians and Fermat too [2]. The suggested proof of Beal’s Conjecture can be related to the part of number theory defined as arithmetic algebraic geometry in spite of that it can be acquired by means of elementary arithmetic operations [2].
Pierre de Fermat formulated his famous proposition on the margin of Diophantus’ “Arithmetic” (near the task 8 of the book II). The eighth problem of the second book asks to separate a square into two squares in whole numbers. It was known long ago that this problem has an infinite set of solutions. But Fermat generalized the task in case of any whole power above the second and pointed out at impossibility of such partition in whole numbers claiming here that he found a “miraculous” proof of this proposition. In order to reconstruct Fermat’s proof it is necessary to understand what Fermat meant by his recording on the margins of Diophantus’ book. So at the very beginning it is a question of fundamental approach to this problem solving by Fermat. Psychologically it is clear that it could be a phenomenological approach when each power of natural numbers is considered as an amount of indivisible multidimensional unit cubes in multidimensional arithmetic space. Thus the task was analogous to the ancient receipt of alchemy: first resolve into elementary units and then put them together in a required manner. “Pure” mathematical unit can be chosen as such elementary unit.
How could Fermat solve this unique problem straight off and without a shadow of doubt ? The sole reason for it is that he saw the mental picture of his proof. Such a picture emerged in his consciousness during his insight allowing him to investigate instantly all necessary details of solution [2]. Visual image of the problem must have had a geometrical form, which apparently could not take its place on narrow margins. This geometric pattern serves as general illustration for Euclid’s theorem about proportional means, from which formulation of Pythagorean theorem and Fermat’s proposition (called Fermat’s Last Theorem later on) could be easily derived. Figure taken from [2] shows stylized design of Euclid’s geometrical theorem on the fractal surface of similar right angle triangles at an instantaneous position of the small diameter of Figure shifting from state Ф1 to state Ф2.
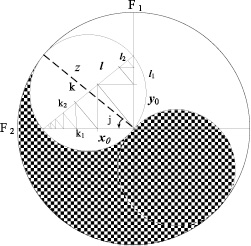
Fig. The designations are explained in the text
Let us proceed following Fermat’s mental investigation of Pythagorean theorem and its generalizations in the case of any n-th degree on splitting higher whole powers into two powers of the same degree. Ancient Greek mathematicians could solve some algebraic equations with only arithmetic methods on the basis of Euclidean geometry, so that they might be called arithmetic geometry methods and included into the range of modern arithmetic algebraic geometry. Of course, Fermat knew about these ancient methods and could develop them using his visual observation of such properties of geometrical figures that became origins for future algebraic notions. But Fermat did not produce new terminology and formulated his research results in pure arithmetic manner. Moreover, his perception of n-th degrees of whole powers was related to Cartesian product of whole numbers from n-dimensional arithmetic space and then each n-th power could be represented as a collection of n-dimensional unit cubes transferred from the state Ф1 to the state Ф2 one by one on the diagram of Figure. This procedure serves as well for finding Pythagorean triples by the method of sorting square units one by one in Pythagorean equation. This method can be applied also to the equation of generalized Fermat’s Last Theorem in order to show that splitting of n-th power of whole numbers into two other powers with n > 2 is impossible. However phenomenological approach described here was not perceived by reviewers of pure mathematical journals and proofs of Beal’s Conjecture and Fermat’s Last Theorem on the indicated phenomenological base were not considered. It was also conditioned by previous acknowledgement of doubtful proofs of Fermat’s Last Theorem in pure mathematics [3; 4].
Solution of Beal’s Conjecture and Fermat’s Last Theorem
The Beal Conjecture states [1]:
The equation Ax + By = Cz has no solution in positive integers A, B, C, x, y, and z with x, y, and z at least 3 and A,B, and C coprime.
Or, restated [1]:
Let A, B, C, x, y, and z be positive integers with x, y, z > 2. If Ax + By = Cz, then A, B, and C have a common factor.
Let us rewrite hypothetical Beal’s Conjecture equality in the following way:
xn + yn = zn, (1)
with positive integers x, y, z having a common factor and exponent n taking simultaneously the next spectrum of values: n = (p, q, m), where integers p, q, m at least 3 and n has one independent value for each term. So we assume at the beginning that equality (1) exists and partitions of the type (1) can be obtained. This method of proof is related to plausible reasoning and called the rule of contraries. Then one can explore some arbitrary solutions of equation (1) in whole numbers.
Consider equality (1) as a partition of whole number zn into two whole parts xn and yn. It resembles Pythagorean equation in real numbers, if we could bring powers in (1) to the degree 2 with whole parts in the similar partition: z2 = xn/ zn–2 + yn/ zn–2. For example, the sacred Egyptian triangle corresponds to the equality: 25 = 16 + 9, that comes of the application of Euclid’s geometrical theorem (see Figure): z = k + l, z2 = z k + z l = xo2 + yo2, 5 = 16/5 + 9/5, 52 = 42 + 32. To produce such scaling, let us introduce the notion of right-angled numbers (these numbers are different from so called right angle triangle numbers representing Pythagorean triples).
Definition. Right-angled number is such a non-negative real number, the square of which is a whole non-negative number.
The set of right-angled numbers Р = {0, 1, √2 , √3 , 2, √5, …} is countable. The system of right-angled numbers P = ⟨Р,+,·,0,1⟩ is defined by operations of addition and multiplication and two singled out elements (zero and unit). The system P is non-closed in relation to addition. Notice that the set of non-negative whole numbers is a subset of the set of right-angled numbers. Then consider (1) on the 2-dimensional lattice of right-angled numbers with coordinates xo , yo, and that, which we call the norms of a right-angled number z assigned to different pairs (xo , yo) and differing from each other by the value of its summands: z2 = xo2 + yo2 (for Egyptian triangle there are 25 such norms: 25 = 1 + 24 = 2 + 23 = …). The norm of non-zero right-angled numbers is always whole and cannot be less than 1. Whole numbers xo2 and yo2 run through values from 1 to z2 and from z2 to 1 one by one. So number z has z2 different partitions as its norms. Similarly any whole power of whole numbers could be expanded to the sum of whole numbers with the aid of right-angled numbers, if we choose the needed common factor in (1). It corresponds to the initial formulation of the problem upon condition that powers in (1) consist of indivisible units. All other possibilities to represent degrees of whole powers using other number systems (for example, rational number systems) are excluded as irrelevant to the formulated problem.
For the purpose of reducing (1) to the view of Pythagorean equation in the system of right-angled numbers, one can rewrite (1) as an equality for some coprime x’, y’, z’, and common whole factor d: (x’d)p + (y’d)q = (z’d)m and fulfil scaling-down:
(z’d)2 = (x’d)p / (z’d)m-2 + (y’d)q / (z’d) m-2 = (x’)p d p–m+2 / (z’)m–2 + (y’)q d q–m+2 / (z’)m–2 = xo2 + yo2,
where xo2 and yo2 with appropriate d are squares of some right-angled numbers xo and yo. If exponents p and q equal m, then d2 can be (z’)2m–4. In other words, we seek such d that satisfy the above stated condition to get whole parts in the sum of this equality. It assumes the following view of (1) after fulfilling scaling-up:
zm = xp + y q = z m–2 (xo2 + yo2). (2)
Let us apply now the ancient method of making powers using Euclid’s geometrical theorem [2] and produce two chains of proportions connected with each other with some equality presenting integer z as a sum of two whole numbers:
z/xo = xo/k = k/k1 = … = k m–3 /k m–2, (3)
z/yo = yo/l = l/l1 = … = l m–3 /l m–2,
where z, xo , yo are right-angled numbers from (2), m natural index at least 3,and z = k + l; k and l are some whole parts of z taken from the method of scaling-down (see below).
From proportions (3) one can obtain the next formulae:
xo2 = kz = (k1z /xo)z,
xo3 = k1z2 = (k2z /xo)z2 , … ,
xom = k m–2 z m–1, (4)
yo2 = lz = (l1z /yo)z ,
yo3 = l1z2 = (l2z /yo)z2 , … ,
yom = lm–2 zm–1,
where integers k and l are found from the basic equality (1):
z = (z’d) = (x’d)p /(z’d) m–1 + (y’d)q /(z’d) m–1 = (x’)p d p-m+1/(z’)m–1 +
+ (y’)q d q-m+1/(z’)m–1 = k + l.
If exponents p and q more or equal m, then numbers k and l are whole with d = (z’)m–1 as a minimum (d can be some whole number divisible by this minimum).
From (2) and (4) we get equal similar partitions of zn into two whole parts:
zm = xp + yq = z m–2(xo2 + yo2) = xm + ym, (5)
hence xp = (xp/m)m = xm, yq = (yq/m)m = ym with whole x, y by construction (for simplicity we do not change here the designations for x, y although exponents p and q are tuple to m). Square roots of xm, ym are mean proportionals between xo2 and zm–2, yo2 and zm–2 describing a bigger right angle triangle defined by the hidden Pythagorean equality zm = xm + ym found from the relations: xm = k z m–1, ym = l z m–1. This implicit triangle is similar to that with sides z, xo, yo represented by equality z2 = xo2 + yo2.
So (1) comes to the Fermat equality (Pythagorean equality in right-angled numbers) that is equivalent to hypothetical phenomenological equality (1);
xm + ym = zm , m ≥ 3, (6)
with whole x = x’d, y = y’d, z = z’d, and some whole factor d that can be expanded into the product of prime factors. One can prove Fermat’s Last Theorem now with the same methods as above in order to obtain solution of the Beal Conjecture in full and one measure.
Let us write Fermat’s Last Theorem in its usual form:
zn = xn + yn, n > 2. (7)
Suppose that one solution at least was found. Then we shall try to construct such a solution and make certain of its impossibility. We shall work in the system of right-angled numbers (see above Definition).
Consider (7) on the 2-dimensional lattice of right-angled numbers with right-angled coordinates x0 , y0 and corresponding norm z2 = x02 + y02 differing by its square fragments relating to definite right-angled coordinates and being a partition of non-zero number z2 into two summands represented by non-negative whole numbers. The minimal (non-zero) norm (standard) of right-angled numbers equals 1.
To construct powers of whole numbers presented in (7), let us produce two chains of continued proportions connected with each other by the norm z2 = x02 + y0 :
z/x0 = x0/k = k/k1 = … = k n–3 /k n–2,
z/y0 = y0/l = l/l1 = … = l n–3/l n–2, (8)
where natural indices of the last terms of each chain in (8) are obtained from n > 2. Continued proportions (8) yield the following formulae:
kz = x02, k1z = x0k, k2z = x0k1, …, kn-2 z = x0k n-3,
lz = y02, l1z = y0l, l2z = y0l1, …, ln-2 z = y0l n-3, (9)
x02 = kz = (k1z /x0)z, x03 = k1z2 = (k2z /x0)z2, … , x0n = kn-2 zn-1,
y02 = lz = (l1z /y0)z, y03 = l1z2 = (l2z /y0)z2, … , y0n = l n-2 z n-1. (10)
It is necessary now to fix the norm for the partition of zn into two like powers in (7). As in the case of Beal’s Conjecture, let us assume that z, x, y in presupposed equality (7) have a common factor d, i. e., z = (z’d), x = (x’d), y = (y’d), where z’, x’. y’ coprime. Thereupon divide equality (7) by zn-1 and get: z = (z’d) = (x’d)n /(z’d)n-1 + (y’d)n /(z’d)n-1 = k + l, where k and l integers with d = (z’)n-1 as a minimum. From this and (9)–(10) it follows that z2 = x02 + y02 and zn = zn-2 (x02 + y02) is a scaled-up modification of the norm z2 = x02 + y02.
Further, one can obtain a singular partition of zn into three terms from (10) for the given norm when n > 2:
zn = x0n + y0n + λn, (11)
where λn = z n-1 [(k – k n-2) + (l – l n-2)] is a remainder after subtracting x0n and y0n out of zn such that λn > 0 when n > 2 and x0 y0 ≠ 0, λn = 0 when n = 2 and x0 y0 ≠ 0, x0, y0,∈ [0, z], z ∈ (0, ∞).
Thus there exists one-to-one correspondence between each pair of numbers (x0, y0) with norm z2 = x02 + y02 from 2-dimensional arithmetic space and each corresponding partition of any whole power with n > 2 of integer z from n-dimensional arithmetic space into the sum of the same powers of numbers x0, y0 and remainder λn from (11). Isomorphism (one-to-one correspondence) between the set of points of 2-dimensional Euclidean space with position vector length z and coordinates x0, y0 , the set of partitions of z2 into squares, and the sets of partitions (11) for any whole n > 2 can be written as follows:
{z ⇒ (xo, yo)} ↔ {z2 = x02 + y02} ↔ {zn = x0n + y0n + λn},
where sets of partitions are generated by the next power similarities:
z ↔ z2 ↔ zn, x0 ↔ x02 ↔ x0n, y0 ↔ y02 ↔ y0n.
Partitions (11) can be reduced to the norm, from which they were obtained:
zn = x0n + y0n + λn = z n-2 (x02 + y02) = xn + yn. (12)
Formula (12) represents by itself a combinatorial equality of two partitions in three and two terms because of the one-to-one correspondence between pairs (x0, y0) and presupposed partition (7). It means that partition (11) coincides with partition (7) if the latter exists. In the case of right-angled numbers this equality is realized only if x0, y0 integers. Algorithm of such correspondence is given in the next formula (13). Thus scaling invariance of the norm z2 = (x02 + y02) leads to the following equalities of different fragments of partitions (12):
x0n + y0n = (xn or yn), (13)
and correspondingly λn = (yn or xn). It can be noticed that x0n ≠ z n-2•y02 = yn and y0n ≠ zn-2•x02 = xn because of the lack of coincidence of decompositions in factorization of numbers x0n and yn, y0n and xn. Obviously, x0n ≠ z n-2•x02 and y0n ≠ zn-2•y02. One can show also that x0 and y0 cannot be irrational in (13) on account of integer partition of zn into xn and yn when n > 2 [2].
Let us come back to the assumption at the beginning of the proof that integer solution (7) exists. This assumption is substantiated only if there is a concrete solution (13) in whole numbers. In order to check the validity of (13) it is necessary to construct it with the same reasoning as before, since equations (7) and (13) are identical by their properties. This procedure can be continued to infinity in the direction of decreasing whole numbers under condition that sequence of different chained equalities never stops and numbers x02 and y02 in (12) will be always whole. If it is not so, i.e., x02 and y02 in chained equalities (13) turn out to be fractions, then this means that solution (7) does not exist in the system of right-angled numbers. Actually, since all partitions of the type (12) are built from the very beginning exclusively on the set of right-angled numbers’ squares being in fact whole items of finite series of partitions, then non-whole x02 and y02 show pointlessness of such procedure, i.e., the absence of integer solution (7) or zero solution. On the other hand, infinite sequence of chained equalities (13) leads to infinite decreasing of positive whole numbers that is impossible and therefore assuming that there exists an integer solution of (7) when n > 2 is not true. Thus the theorem is proved both for all even and for all odd degrees of whole numbers and for any finite whole x, y, z, d.
Conclusion
Beal’s Conjecture solution contains in itself the description of a new hypothetical mathematical object with simple properties conditioned only by its intrinsic structure. One can see this structure formed from similar right angle triangles obtained with the aid of Pythagorean triples z, x0, y0 characterizing hypothetical partition (7) on the diagram of Figure. This hypothetical mathematical object represents by itself a closed cycle of identical transformations of one and the same partition zn = xn + yn:
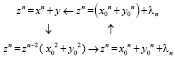
Equality of the above partitions is substantiated only by suggestion that whole power n > 2 can be divided into two whole parts that leads automatically to similarity and equality in itself of one and the same partition given in the form of two or three terms.
However generalized Fermat’s Last Theorem states that it is impossible to construct partition (1) or (7) into other n-th powers of whole numbers when n > 2. Applying the rule of contraries we claim that if such partitions exist then partitions (13) exist as well. Construction of (13) leads in total to a zero result and therefore generalized Fermat’s Last Theorem can be regarded as a mathematical discovery running ahead of its proof.
Beal’s Conjecture can be also considered at the level of metamathematics when it is necessary to choose an adequate number system for solution of this problem. In the given case such an adequate number system was the system of right-angled numbers. This system have many interesting applications in natural sciences [2]. In particular, it participates in forming a surface fractal consisted of decreasing right angle triangles and revealed in quantum physics applications.
In conclusion we suppose that contemporary theoretical science seemed to be exhausted in its description of real world and new alternative bases of physics, chemistry, and other disciplines should be searched. These bases can be found by studying the diagram of Figure representing kinematics and dynamics of any interaction processes in nature. One can begin for example at that all school trigonometry can be considered and described in visual language of potential geometrical constructions of Figure. Moreover, outstanding progress is expected in quantum informatics using quantum (phenomenological, in our terminology) approach in analogue computation of 3-dimensional space states described by a 4-dimensional space sphere according to the Poincare Conjecture and conditionally represented on Figure [2]. Thus any objective reality can be adequately described with the aid of right mathematical perception leading to broadening of human consciousness and therefore discovering new possibilities in new fields of knowledge. It means that such quantum approach will allow to equate human perception with real physical and other natural processes.

