It was showed [38–40], the deterministic modular structures with necessary dimensional and spectral module’s characteristics are may be formed into certain cellular 2D or 3D space. Characteristics of these structures are may be determined from structural states descriptions and used for interpretation of the peculiarities of the phase distributions and inter-phase borders configurations onto surface and into volume of the compositional materials [1–6]. The analysis results of the possible types of structural states are necessary for influence calculation of the dimension parameter on some additive properties of the corresponding material [7–9].
Formally the “hyper-spatial” description of the possible structural states determined the values of the effective dimensional parameter of compositional materials and corresponding chemical and physic-mechanical properties is include the symbolic description of (r r r) from crystal component, the state (n n n) from nano-dimension component and the state (f f f) from fractal component of the composite [10–12]. The description of the last state consist the information about the possible quasi-fractal configurations of the inter-phase borders (f f f)3Dconf, which are the 3D shall of the system of elements of analyzed deterministic modular structures with corresponding fractal states, about the possible quasi-fractal 3D elements distributions onto sites of modular structures (f f f)site = (f f f)*, and about the possible quasi-fractal 3D distributions of the r and n elements on sizes [(r r r)f, + (n n n)f]size.
Crystal nano-dimensional fractal class RNF is the unique class contained the all types of the state components which presented in description of the some compositional material:
[(r r r), (n n n), (f f f)3D conf , (f f f)*site, ((r r r)f +(n n n)f)size]).
Therefore, the combinatorial search of all possible structural states of this class and a description of them are relevant to the preliminary assessment of the influences of dimension parameter on the volumetric or superficial characteristics of the analyzed composite.
If the possible continual components of the states t are use then for ultrafine composite materials can be viewed the amorphous structural elements of some nano-structured heterogeneous object.
The formalism of the presence of continual components in structural state description is may be regards as a method of realization of the deterministic structures splitting on substructures with continual 1D and 2D borders. Continual 1D and 2D elements are may be considered as a conditional borders between structural modules, module blocks, layers and other modules associates are formally presents in structures of some ordered and disordered solid solutions [13–18, 44], in structures of the members of some homological series [13–17, 36, 37, 41, 42], into composites and heterogenic structures [43]. Note that the results of the analysis of possible structural conditions of (RNF) class are necessary in order to take account of the impact of dimension option on some additive properties of the corresponding nano-structured composite material [7–9].
Thus, the need to analyses of the possible structural states of the objects of (RNF) class not only with discrete but and continual elements are obvious.
Analysis of the possible dis-continual structural states
Taking into account the elements of discrete {ti} groups of translations (i = 1, 2, 3) the main subclasses of apparent structural states of crystal nano-fractal objects into 3D space are may be obtained [3, 4, 14, 19]. It is anticipated that all local elements of these states (fragment r, nano-structured fragment rn, fractal f, fractal fragment rf, local fractal fr, nano-structured fractal fn, nano-particle n, nano-fragment nr or nano-fractal nf) are asymmetrical elements. Therefore, partial or full disordering of these elements will consider the deterministic modular structure type R3s,0 . Indexes s and 0 in the designation of the structure are means the number of independent crystallographic directions in which the asymmetric elements of positional and orientation are ordered in 3D space.
Cite brief compared with [20–22] description of the possible structural states for the abstract fractal crystal nano-dimensional 3D objects.
Crystal nano-dimension fractal class (18 subclasses, 210 states by type (r n f) or its derivatives).
1. Subclass RNF:
– 27 states by type (r n f) from ordered chains of different fragments, nano-particles and Fractals: (r n f), (r n fr), (r n fn), (r nr f), (r nr fr), (r nr fn), (r nf f), (r nf fr), (r nf fn), (rn n f), (rn n fr), (rn n fn), (rn nr f), (rn nr fr), (rn nr fn), (rn nf f), (rn nf fr), (rn nf fn), (rf n f), (rf n fr), (rf n fn), (rf nr f), (rf nr fr), (rf nr fn), (rf nf f), (rf nf fr), (rf nf fn).
2. Subclass RNF0:
– 9 states by type (r n f0) from ordered chains of different fragments, nano-particles and quasi-chains of Fractals: (r n f0), (r nr f0), (r nf f0), (rn n f0), (rn nr f0), (rn nf f0), (rf n f0), (rf nr f0), (rf nf f0),
– 9 states by type (r n0f) from ordered chains of different fragments, Fractals and quasi-chains of nano-particles: (r n0 f), (r n0 fr), (r n0 fn), (rn n0 f), (rn n0 fr), (rn n0 fn), (rf n0 f), (rf n0 fr), (rf n0 fn),
– 9 states by type (r0n f) from ordered chains of different Fractals, nano-particles and quasi-chains of fragments: (r0 n f), (r0 n fr), (r0 n fn), (r0 nr f), (r0 nr fr), (r0 nr fn), (r0 nf f), (r0 nf fr), (r0 nf fn).
3. Subclass RNF00:
– 3 states by type (r n0f0) from chains of different fragments and quasi-chains of nano-particles and Fractals: (r n0 f0), (rn n0 f0), (rf n0 f0),
– 3 states by type (r0n f0) from chains of different nano-particles and quasi-chains of fragments and Fractals: (r0 n f0), (r0 nr f0), (r0 nf f0),
– 3 states by type (r0n0f) from chains of different Fractals and quasi-chains of fragments and nano-particles: (r0 n0 f), (r0 n0 fr), (r0 n0 fn).
4. Subclass RNF000:
– 1 state by type (r0n0f0) from quasi-chains of ordered Fractals, fragments and nano-particles.
5. Subclass a-periodic RNFs:
– 9 states by type (r n fs) from chains of different ordered fragments, nano-particles and chains of the disordered Fractals: (r n fs), (r nr fs), (r nf fs), (rn n fs), (rn nr fs), (rn nf fs), (rf n fs), (rf nr fs), (rf nf fs),
– 9 states by type (r nsf) from chains of different ordered fragments, Fractals and chains of the disordered nano-particles: (r ns f), (r ns fr), (r ns fn), (rn ns f), (rn ns fr), (rn ns fn), (rf ns f), (rf ns fr), (rf ns fn),
– 9 states by type (rsn f) from chains of different ordered nano-particles, Fractals and chains of the disordered fragments: (rs n f), (rs n fr), (rs n fn), (rs nr f), (rs nr fr), (rs nr fn), (rs nf f), (rs nf fr), (rs nf fn).
6. Subclass twice a-periodic RNFss:
– 3 states by type (r nsfs from chains of different fragments and the disordered nano-particles and Fractals: (r ns fs), (rn ns fs), (rf ns fs),
– 3 states by type (rsn fs) from chains of different nano-particles and the disordered fragments and Fractals: (rs n fs), (rs nr fs), (rs nf fs),
– 3 states by type (rsnsf) from chains of different Fractals and the disordered fragments and nano-particles: (rs ns f), (rs ns fr), (rs ns fn).
7. Subclass thrice a-periodic RNFsss:
– 1 state by type (rsnsfs) from chains of different disordered Fractals, fragments and nano-particles.
8. Subclass a-periodic RNF0s*:
– 9 states by type (r n f0s) from chains of different ordered fragments, nano-particles and the quasi-chains of the disordered Fractals: (r n f0s), (r nr f0s), (r nf f0s), (rn n f0s), (rn nr f0s), (rn nf f0s), (rf n f0s), (rf nr f0s), (rf nf f0s),
– 9 states by type (r n0sf) from chains of different fragments, Fractals and the quasi-chains of the disordered nano-particles: (r n0s f), (r n0s fr), (r n0s fn), (rn n0s f), (rn n0s fr), (rn n0s fn), (rf n0s f), (rf n0s fr), (rf n0s fn),
– 9 states by type (r0sn f) from chains of different nano-particles, Fractals and the quasi-chains of the disordered fragments: (r0s n f), (r0s n fr), (r0s n fn), (r0s nr f), (r0s nr fr), (r0s nr fn), (r0s nf f), (r0s nf fr), (r0s nf fn).
9. Subclass a-periodic RNF0s:
– 3 states by type (rn0fs) from chains of different fragments, the disordered Fractals and the quasi-chains of the nano-particles: (r n0 fs), (rn n0 fs), (rf n0 fs),
– 3 states by type (rnsf0) from chains of different fragments, the disordered nano-particles and the quasi-chains of the Fractals: (r ns f0), (rn ns f0), (rf ns f0),
– 3 states by type (r0n fs) from chains of different nano-particles, the disordered Fractals and the quasi-chains of the fragments: (r0 n fs), (r0 nr fs), (r0 nf fs),
– 3 states by type (rsn f0) from chains of different nano-particles, the disordered fragments and the quasi-chains of the Fractals: (rs n f0), (rs nr f0), (rs nf f0),
– 3 states by type (r0nsf) from chains of different Fractals, the disordered nano-particles and the quasi-chains of the fragments: (r0 ns f), (r0 ns fr), (r0 ns fn),
– 3 states by type (rsn0f) from chains of different Fractals, the disordered fragments and the quasi-chains of the nano-particles: (rs n0 f), (rs n0 fr), (rs n0 fn).
10. Subclass twice a-periodic RNF0ss*:
– 3 states by type (rn0sfs from chains of different fragments, the disordered Fractals and the quasi-chains of the disordered nano-particles: (r n0s fs), (rn n0s fs), (rf n0s fs),
– 3 states by type (rnsf0s) from chains of different fragments, the disordered nanoparticles and the quasi-chains of the disordered Fractals: (r ns f0s), (rn ns f0s), (rf ns f0s),
– 3 states by type (r0snfs) from chains of different nano-particles and the disordered Fractals, the quasi-chains of the disordered fragments: (r0s n fs), (r0s nr fs), (r0s nf fs),
– 3 states by type (rsnf0s) from chains of different nano-particles and the disordered fragments, the quasi-chains of the disordered Fractals: (rs n f0s), (rs nr f0s), (rs nf f0s),
– 3 states by type (r0snsf) from chains of different Fractals and the disordered nano-particles, the quasi-chains of the disordered fragments: (r0s ns f), (r0s ns fr), (r0s ns fn),
– 3 states by type (rsn0sf) from chains of different Fractals and the disordered fragments, the quasi-chains of the disordered nano-particles: (rs n0s f), (rs n0s fr), (rs n0s fn.
11. Subclass a-periodic RNF00s*:
– 3 states by type (r n0 f0s) from chains of different fragments, the quasi-chains of the nano-particles and the disordered Fractals: (r n0 f0s), (rn n0 f0s), (rf n0 f0s),
– 3 states by type (r n0s f0) from chains of different fragments, the quasi-chains of the Fractals and the disordered nano-particles: (r n0s f0), (rn n0s f0), (rf n0s f0),
– 3 states by type (r0nf0s) from chains of different nano-particles, quasi-chains of the fragments and the disordered Fractals: (r0 n f0s), (r0 nr f0s), (r0 nf f0s),
– 3 states by type (r0snf0) from chains of different nano-particles, the quasi-chains of the Fractals and the disordered fragments: (r0s n f0), (r0s nr f0), (r0s nf f0),
– 3 states by type (r0n0sf) from chains of different Fractals, quasi-chains of the fragments and the disordered nano-particles: (r0 n0s f), (r0 n0s fr), (r0 n0s fn),
– 3 states by type (r0sn0f) from chains of different Fractals, the quasi-chains of the nano-particles and the disordered fragments: (r0sn0 f), (r0s n0 fr), (r0s n0 fn).
12. Subclass a-periodic RNF00s:
– 1 state by type (r0 n0 fs) – the chains of the disordered Fractals, the quasi-chains of the fragments and nano-particles,
– 1 state by type (r0 ns f0) – the chains of the disordered nano-particles, the quasi-chains of the fragments and Fractals,
– 1 state by type (rs n0 f0) – the chains of the disordered fragments, the quasi-chains of the nano-particles and Fractals.
13. Subclass twice a-periodic RNF0ss:
– 1 state by type (r0 ns fs) – the chains of the disordered nano-particles and Fractals, the quasi-chains of the fragments,
– 1 state by type (rs n0 fs) – the chains of the disordered fragments and Fractals, the quasi-chains of the nano-particles,
– 1 state by type (rs ns f0) – the chains of the disordered fragments and nano-particles, the quasi-chains of the Fractals.
14. Subclass twice a-periodic RNF00ss**:
– 3 states by type (r n0sf0s) from the quasi-chains of the disordered nano-particles and Fractals, the chains of different fragments: (r n0s f0s), (rn n0s f0s), (rf n0s f0s),
– 3 states by type (r0sn f0s) from the quasi-chains of the disordered fragments and Fractals, the chains of different nano-particles: (r0s n f0s), (r0s nr f0s), (r0s nf f0s),
– 3 states by type (r0sn0sf) from the quasi-chains of the disordered fragments and nano-particles, the chains of different Fractals: (r0s n0s f), (r0s n0s fr), (r0s n0s fn).
15. Subclass twice a-periodic RNF00ss*:
– 1 state by type (r0s n0 fs) – the quasi-chains of nano-particles and the disordered fragments, the chains of the disordered Fractals,
– 1 state by type (r0s ns f0) – the quasi-chains of Fractals and the disordered fragments, the chains of the disordered nano-particles,
– 1 state by type (r0 n0s fs) – the quasi-chains of the fragments and the disordered nano-particles, the chains of the disordered Fractals,
– 1 state by type (rs n0s f0) – the quasi-chains of Fractals and the disordered nano-particles, the chains of the disordered fragments,
– 1 state by type (r0 ns f0s) – the quasi-chains of the fragments and the disordered Fractals, the chains of the disordered nano-particles,
– 1 state by type (rs n0 f0s) – the quasi-chains of nano-particles and the disordered Fractals, the chains of the disordered fragments.
16. Subclass twice a-periodic RNF000ss**:
– 1 state by type (r0s n0s f0) – the quasi-chains of Fractals and the disordered fragments and nano-particles,
– 1 state by type (r0s n0 f0s) – the quasi-chains of nano-particles and the disordered fragments and Fractals,
– 1 state by type (r0 n0s f0s) – the quasi-chains of the fragments and the disordered nano-particles and Fractals.
17. Subclass thrice a-periodic RNF00sss**:
– 1 state by type (r0s n0s fs) – the quasi-chains of the disordered fragments and nano-particles, the chains of the Fractals,
– 1 state by type (r0s ns f0s) – the quasi-chains of the disordered fragments and Fractals, the chains of the nano-particles,
– 1 state by type (rs n0s f0s) – the quasi-chains of the disordered nano-particles and Fractals, the chains of the fragments.
18. Subclass thrice a-periodic RNF000sss***:
– 1 state by type (r0sn0sf0s) – the quasi-chains of the disordered fragments, nano-particles and Fractals.
Thus, the descriptions of the complex structural states of deterministic modular structures, quasi-structures and a-periodic structures that contain the crystalline, nano-dimension and fractal components in the form of asymmetric modules, fully or partially ordered into 3D space were received.
Classification of continuous structural states
Taking into account the elements of discrete {τi} and continuous group of translations {τi} (i = 1, 2, 3) the main subclasses of apparent structural states of crystal nano-fractal objects into 3D space are may be obtained [23, 24].
1D continual RNF class (10 subclasses, 108 states).
1. Subclass RNFt:
– 9 states by type (τ n f) – 1D continuum, the chains of the different nano-particles и fractals: (τ n f), (τ n fr), (τ n fn), (τ nr f), (τ nr fr), (τ nr fn), (τ nf f), (τ nf fr), (τ nf fn),
– 9 states by type (r τ f) – the chains of the different fragments and fractals, 1D continuum: (r τ f), (r τ fr), (r τ fn), (rn τ f), (rn τ fr), (rn τ fn), (rf τ f), (rf τ fr), (rf τ fn),
– 9 states by type (r n τ) – the chains of the different fragments and nano-particles, 1D continuum: (r n τ), (r nr τ), (r nf τ), (rn n τ), (rn nr τ), (rn nf τ), (rf n τ), (rf nr τ), (rf nf τ).
2. Subclass RNF0t:
– 3 states by type (τ n f0) – 1D continuum, the chains of the different nano-particles and the quasi-chains of the fractals: (t n f0), (τ nr f0), (τ nf f0),
– 3 states by type (r τ f0) – the chains of the different fragments, 1D continuum and the quasi-chains of the fractals: (r τ f0), (rn τ f0), (rf τ f0),
– 3 states by type (r n0 τ) – the chains of the different fragments and the quasi-chains of the nano-particles, 1D continuum: (r n0 τ), (rn n0 τ), (rf n0 τ),
– 3 states by type (τ n0f) – 1D continuum, the chains of the different fractals and the quasi-chains of the nano-particles: (τ n0 fr), (τ n0 fn), (τ n0 f),
– 3 states by type (r0 τ f) – the chains of the different fractals, 1D continuum and the quasi-chains of the fragments: (r0 τ f), (r0 τ fr), (r0 τ fn),
– 3 states by type (r0n τ) – the chains of the different nano-particles and the quasi-chains of the fragments, 1D continuum: (r0 nr τ), (r0 n τ), (r0 nf τ).
3. Subclass RNF00t:
– 1 state (τ n0 f0) – 1D continuum, the quasi-chains of the nano-particles and fractals,
– 1 state (r0 τ f0) – 1D continuum, the quasi-chains of the fragments and fractals,
– 1 state (r0 n0 τ) – 1D continuum, the quasi-chains of the fragments and nano-particles.
4. Subclass a-periodic RNFst:
– 3 states by type (τ n fs) – 1D continuum, the chains of the different nano-particles and the disordered fractals: (τ n fs), (τ nr fs), (τ nf fs),
– 3 states by type (r t fs) – 1D continuum, the chains of the different fragments and the disordered fractals: (r τ fs), (rn τ fs), (rf τ fs),
– 3 states by type (τ ns f) – 1D continuum, the chains of the different fractals and the disordered nano-particles: (τ ns f), (τ ns fr), (t ns fn),
– 3 states by type (r ns τ)– the chains of the different fragments and the disordered nano-particles, 1D continuum: (r ns t), (rn ns τ), (rf ns τ),
– 3 states by type (rs τ f) – the chains of the different fractals and the disordered fragments, 1D continuum: (rs τ f), (rs τ fr), (rs τ fn),
– 3 states by type (rsn τ) – the chains of the different nano-particles and the disordered fragments, 1D continuum: (rs n τ), (rs nr τ), (rs nf τ).
5. Subclass twice a-periodic RNFsst:
– 1 state (τ ns fs) – 1D continuum and the disordered nano-particles and fractals,
– 1 state (rs τ fs) – 1D continuum and the disordered fragments and fractals,
– 1 state (rs ns τ) – 1D continuum and the disordered fragments and nano-particles.
6. Subclass a-periodic RNF0st*:
– 3 states by type (τ n f0s) – 1D continuum, the chains of the different nano-particles and the quasi-chains of the disordered fractals: (τ n f0s), (τ nr f0s), (τ nf f0s),
– 3 states by type (r τ f0s) – the chains of the different fragments, 1D continuum and the quasi-chains of the disordered fractals: (r τ f0s), (rn τ f0s), (rf τ f0s),
– 3 states by type (r n0s τ) – the chains of the different fragments and the quasi-chains of the disordered nano-particles, 1D continuum: (r n0s τ), (rn n0s τ), (rf n0s τ),
– 3 states by type (τ n0sf) – 1D continuum, the chains of the different fractals and the quasi-chains of the disordered nano-particles: (τ n0s fr), (τ n0s fn), (τ n0s f),
– 3 states by type (r0st f) – the chains of the different fractals, 1D continuum and the quasi-chains of the disordered fragments: (r0s τ f), (r0s τ fr), (r0s τ fn),
– 3 states by type (r0sn τ) – the chains of the different nano-particles and the quasi-chains of the disordered fragments, 1D continuum: (r0s nr τ), (r0s n τ), (r0s nf τ).
7. Subclass a-periodic RNF0st:
– 1 state (t n0 fs) – 1D continuum, the chains of the disordered fractals and the quasi-chains of the nano-particles,
– 1 state (t ns f0) – 1D continuum, the chains of the disordered nano-particles and the quasi-chains of the fractals,
– 1 state (r0 τ fs) – the chains of the disordered fractals, 1D continuum and the quasi-chains of the fragments,
– 1 state (rs τ f0) – the chains of the disordered fragments, 1D continuum and the quasi-chains of the fractals,
– 1 state (r0 ns τ) – the chains of the disordered nano-particles and the quasi-chains of the fragments, 1D continuum,
– 1 state (rs n0 τ) – the chains of the disordered fragments and the quasi-chains of the nano-particles, 1D continuum.
8. Subclass twice a-periodic RNF0sst*:
– 1 state (τ n0s fs) – 1D continuum, the chains of the disordered fractals and the quasi-chains of the disordered nano-particles,
– 1 state (τ ns f0s) – 1D continuum, the chains of the disordered nano-particles and the quasi-chains of the disordered fractals,
– 1 state (r0s τ fs) – the chains of the disordered fractals, 1D continuum and the quasi-chains of the disordered fragments,
– 1 state (rs τ f0s) – the chains of the disordered fragments, 1D continuum and the quasi-chains of the disordered fractals,
– 1 state (r0s ns τ) – the chains of the disordered nano-particles and the quasi-chains of the disordered fragments, 1D continuum,
– 1 state (rs n0s τ) – the chains of the disordered fragments and the quasi-chains of the disordered nano-particles, 1D continuum.
9. Subclass a-periodic RNF00st*:
– 1 state (τ n0 f0s) – 1D continuum, the quasi-chains of the nano-particles and the disordered fractals,
– 1 state (τ n0s f0) – 1D continuum, the quasi-chains of the fractals and the disordered nano-particles,
– 1 state (r0 τ f0s) – 1D continuum, the quasi-chains of the fragments and the disordered fractals,
– 1 state (r0s τ f0) – 1D continuum, the quasi-chains of the fractals and the disordered fragments,
– 1 state (r0 n0s t) – the quasi-chains of the fragments and the disordered nano-particles, 1D continuum,
– 1 state (r0s n0 τ) – the quasi-chains of the nano-particles and the disordered fragments, 1D continuum.
10. Subclass twice a-periodic RNF00sst**:
– 1 state (τ n0s f0s) – 1D continuum, the quasi-chains of the disordered nano-particles and the fractals,
– 1 state (r0s τ f0s) – the quasi-chains of the disordered fragments and the fractals, 1D continuum,
– 1 state (r0s n0s τ) – the quasi-chains of the disordered fragments and the nano-particles, 1D continuum.
2D continual RNF class (4 subclasses, 18 states).
1. Subclass RNFtt:
– 3 states by type (τ τ f) from the 2D continuum and the chains of the different fractals: (τ τ f), (τ τ fr), (τ τ fn),
– 3 states by type (r τ τ) from the chains of the different fragments and the 2D continuum: (r τ τ), (rn τ τ), (rf τ τ),
– 3 states by type (τ n τ) from the chains of the different nano-particles and the 2D continuum: (t n τ), (τ nr τ), (τ nf τ).
2. Subclass RNF0tt:
– 1 state (τ τ f0) – 2D continuum, the quasi-chains of the fractals,
– 1 state (τ n0 τ) – the quasi-chains of the nano-particles, 2D continuum,
– 1 state (r0 τ τ) – 2D continuum, the quasi-chains of fragments,
3. Subclass a-periodic RNFstt:
– 1 state (τ τ fs) – 2D continuum, the chains of the disordered fractals,
– 1 state (τ ns τ) – 2D continuum, the chains of the disordered nano-particles,
– 1 state (rs τ τ) – the chains of the disordered fragments, 2D continuum,
4. Subclass a-periodic RNF0stt*:
– 1 state (τ τ f0s) – 2D continuum, quasi-chains of the disordered fractals,
– 1 state (τ n0s τ) – quasi-chains of the disordered nano-particles, 2D continuum,
– 1 state (r0s τ τ) – 2D continuum and the quasi-chains of the disordered fragments.
3D continual RNF class (1 subclass, 1 state).
Subclass RNFτττ,:
– 1 state (τ τ τ) – 3D continuum, formally it’s not a structural state.
Discussion of the results
As the RNF class is contain the all kinds of state components, a set of descriptions of states (r n f) can be seen as the abstract full folding “hyper-spatial” description of the material [25, 26]:
[(r r r), (n n n), (f f f)3D conf, (f f f)*site, ((r r r)f +(n n n)f)size]).
Indeed, if transposed of matrix from three arbitrary states by type (r n f) can always get the three relevant states from the crystalline, nano-dimension and fractal components:
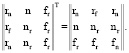
The consideration of the conjugate to fractal states (fr fr fn)*site = (rf rf nf) and the states with r and n components, distributed by fractal law, is contain the information about dimension of quasi-fractal distributions of the relevant component.
All this information is necessary when evaluating conditional dimension parameter Di for each i-th structural 3D state by the formula
Di = 0,5(dr D(r) + df D(f) + dn D(n))i,
were dr, df and dn – are the numbers of the relevant component of the same grade. The dimension parameter for crystalline component is D(r) = 1, for the fractal component is the fractal dimension:
D(f) = DimRf = Dim (GenRf) < 1,
for nano-dimensional component D(n) = (<n>/no) < 1, if the average size of the nano-object <n> is smaller, then no = 100 nm [7–9].
It can be assumed that some of these structural states of the type (r n f) are may describe the results of manifestations of the specific phase-disordered state onto surface of composite materials and coatings [2, 5, 6, 27–30]. The results of the analysis of these states were, in particular, used in determining of the level of synergies for some composite coatings by friction and wear [31–35, 45, 46].
In this work was showed a concept possibility of existence of the 1D-continuum containing complex structural states for crystal nano-dimension objects, for crystal fractals and nano-fractals, as well as the 2D continuum containing complex structural states of crystalline, nano-dimension and fractal objects. It is anticipated that some of these structural states may be characteristic of the some composites with heterogeneous structures.
Conclusion
The organization peculiarities of the possible states for deterministic modular structures of the crystal-nano-dimension fractal objects of the (RNF) class with discrete components were reviewed.
The states classification of crystalline nano-fractal structures, including the 1-, 2- and 3-a-periodic structural states, the 1-, 2- and 3-quazi-structural states, the 1D- and 2D-continuum containing complex states and possible its combinations was proposed.
The possibility of the existence of the 336 complex structural states, including the 108 states with 1D continuum and 18 states – with 2D continuum was showed.
It is anticipated that some of these structural states may characterize the certain phase-disordered states of multi-phase materials and formally considered as a 3D convolution of “hyper-spatial” representation on crystalline, nano-dimension and fractal structural states of composites and materials with heterogeneous structures.

