Scientific journal
European Journal of Natural History
ISSN 2073-4972
ИФ РИНЦ = 0,301

Personal portfolio

THE MATHEMATICAL COMPETENCE MODEL IN ASPECT OF STUDYING E-LEARNING EFFICIENCY

Snegireva L.V. 1
1 Kursk State Medical University
Article in PDF
1853 KB
1. Snegireva L.V. E-learning as an instrument of students’ generalization skills development // Modern high technologies. – 2016. – № 6–2. – P. 416–420.
2. Snegireva L.V. The formation of the main structural components of medical students’ mathematical competence throughout the e-learning process// Modern high technologies. – 2016. – № 8–2. – P. 363–367.
3. Shaldybina O.N. Essence of mathematical competence of students // Continuous psychology and pedagogical education: problems, searches, prospects: Materials of the International scientific and practical conference: in 2 h / Under the editorship of R.A. Valeeva, G.Zh. Fakhrutdinova. – Kazan: TGGPU, 2009. – P. 1. – P. 217–222.
4. Snegireva L.V. The e-learning as an instrument of medical students’ mathematical abilities development// Modern problems of science and education. – 2016. – № 3; URL: http://www.science-education.ru/article/view id=24493 (the date of access: 13.05.2016).
5. Pakharenko N.V., Zolnikov I.N. model of determination of level of formation of common cultural and professional competences//Modern problems of science and education. – 2012. – № 6. URL: http://www.science-education.ru/ru/article/view id=7502 (date of the address: 12.06.2016).
6. Nalivayko T.E., Shinkoruk M.V. Theoretical justification of system of criteria and indicators of formation of kompetentnost of students//Scientists of a note of Komsomolsk-on-Amur state technical university. – 2013. – № 1 (13). Volume 2. – P. 23–30.

The article contains the results of elaboration of three-dimensional mathematical competence model. The author of the article provides that the suggested model represents the real university students’ mathematical competence development level and its separate components, providing various factors influence studying on process of mathematical competence formation. The model is easily realized in educational process. The model can surely be used in practice.

To the opinion of modern pedagogical researchers, mathematical competence is students’ personal integrative characteristic, including mathematical base for studying biological and medical subjects and also students’ ability to use the mathematical knowledge for solving the professional practical tasks and theoretical problems [1, 2]. Mathematical competence has the complicated multicomponent structure [3, 4]. Cognitive, performing, motivational and personal mathematical competence components are the base of modern mathematical competence model [5]. Each of mathematical competence structural components demands its own criteria and indicators system [6], that rather difficult to realize in practice. In this regard, functional components mathematical competence model elaboration was defined as our research aim.

Research tasks are:

  • analysis of mathematical competence structural components;
  • elaboration of three-dimensional mathematical competence model.

Medical university clinical psychology students’ mathematical competence was chosen as the research object.

Materials and methods. The testing of second-year clinical psychology students was carried out. 10 second-year clinical psychology faculty students were involved into mathematical e-learning testing after passing the mathematical course examination. The research was held at 11 a.m. in the academic auditory. The research duration was about 50 minutes. The clinical psychology faculty students performed the testing independently without using any electronic devices. The testing was built on the basis of Atmhauer intelligence structure test including the scale of mathematical abilities determination and a questionnaire “Thinking type”.

To solve mathematical task the examinee is to be ready to demonstrate firstly his ability to analysis and synthesis, including

  • to allocate various elements in its structure;
  • to give them an assessment;
  • to systematize;
  • to define hierarchy.

Secondly, the ability of manipulating abstract symbols and concepts is required. Hypothesis and strategy of solution also have the abstract form for examinee. Thirdly, students’ ability to generalization is necessary condition of mathematical tasks solving.

It’s known, that mathematical task assumes specific conditions, and big variety of the same task in fact is possible. Respectively, the task solving strategy always has the generalized character.

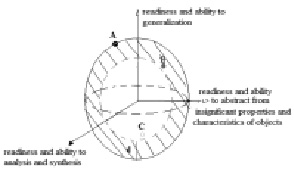
snegir1.tif

Three-dimensional representation of model of mathematical competence

Thus, the successful mathematical tasks solving requires three cognitive components possession:

  • readiness and ability to analysis and synthesis;
  • readiness and ability to abstract from insignificant properties and characteristics of objects;
  • readiness and ability to generalization.

The listed components, in our opinion, can be considered as the mathematical competence main structural components based on cognitive, performing, motivational and personal mathematical competence. Taking into consideration these three functional components, we can represent the mathematical competence model in three-dimensional space (figure).

The main functional components are used as coordinate axes of medical students’ mathematical competence model: K1, K2 and K3, where K1 – is readiness and ability to the analysis and synthesis, K2 – readiness and ability to abstract from insignificant properties and characteristics of objects, K3 – readiness and ability to generalization.

Each functional component has its own contribute into the level of students’ mathematical competence. The received level of students’ mathematical competence is realized as a point of a sphere according to the equation:

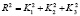sneg01.wmf. (1)

External sphere radius Rexternal is calculated according to the formula:

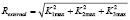sneg02.wmf. (2)

K1max, K2max and K3max are the maximal possible level in each mathematical competence component respectively.

Internal sphere radius Rinternal is found from the expression:

Rinternal = 0,6 Rexternal. (3)

Thickness of sphere layer d is determined by the formula:

d = Rexternal – Rinternal. (4)

The sphere space between internal and external radii points medical school students’ mathematical competence level corresponding to educational standard. The points inside the sphere out of chosen area indicate insufficient level of students’ mathematical competence.

We consider that the suggested mathematical competence model can serve as the additional tool of students’ mathematical competence level assessment, supplementing and expanding the criteria and indicators systems.

The work is submitted to the International Scientific Conference «Science and education in contemporary Russia » Moscow, November 15–16, 2016, came to the editorial office оn 05.11.2016.