The questions of condition analysis and prognosis of the development of the whole education system and each single educational institution have a great significance. It is conditioned by a number of reasons, and the major one is that education, being conservative in a certain way, does not meet the modern requirements of the scientific-technical progress. Some even speak of a crisis within education in modern world. While predicting education development trends, many often restrict it to an abstract theory statement and broad generalizations that are distant from reality. So, measures, taken to improve the education system often prove to be low-effective.
An achievement of a positive effect in taking measures, aimed for the education system improvement, as we think, is possible only in case of an education development concept development that would be based, first of all, on knowledge what «a student» in its general meaning and how he interacts , for example, with a professor-tutor personnel of an institution. A concept should also include a strategy of the whole education system reforming strategy, aimed for the securing of optimal conditions for each student creative abilities. A definite help in the solution of the described problem can be provided by an education process probabilistic-statistic modeling method [1]. Let us study the mian aspects of this method.
Determinism and randomness of a cognition process
A quantity and quality of the information, processed and learned by a man within a cognition process is condition by his mind development level. The study of the human mind phenomenons forms an extremely difficult objective. It is related on principle to the direct non-observability of its mechanisms. Within the cognition structure we can include such cognitive processes as sensation, perception, memory, thinking, imagination. The analysis of these processes shows that they carry elements of uncertainty and randomness that are conditioned by a principle non-repeatability of a full-scale person´ psychosomatic condition and environment conditions from one experiment to another, and also physiological, psychological, and information noises in a brain activity. The latter led to the denial of determinist dynamic model usage within the thinking process description and the accepting of the random dynamic system model.
From the described above it is obvious that a mind determinism that expresses in the objective reality reflection within a man´s brain is realized through randomness. Therefore we can conclude, that a man´s knowledge, being, in fact, a product of mind, also carry random character. So, to describe a cognition process one can use the probabilistic-statistic method [1, 2].
A student model
In [1] a student probabilistic-statistic model is developed in accordance with which a person within the process of his education moves within informative space. However, as a man´s knowledge carries elements of uncertainty and randomness, it proves impossible to define a student´s definite location in informative space. It is only possible to speak of his probable location in one of another part of it. In this model each individual is identified by a distribution function (probability density) - a probability to allocate him in a single information space area. Within an education process a distribution function that identifies a student, evolving, moves within the informative space. Each student has individual properties and independent localization (areal and kinematic) of individuals is possible.
According to the law of probability saving a system of differential equations has been written down. They are continuity equations that link probability density alteration per a time unit it phase space (space of coordinates and kinematic units of different orders) with the probability density flow divergence in the studied phase space. When the distribution function that for any random individual depends only on coordinates and time, the continuity equation looks as follows
(1)
where 
is the probability density in the coordinate system; 
is the probability density in coordinate and speed space; σ is a coordinate in the informative space; 
is speed; 
is avarage speed; t is time.
In [1] we have obtained the following equation solution (1):
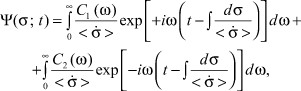(2)
where w is frequency rate; C1(ω) and C2(ω) are integration constants, dependent on ω, and normnormalized for a singular frequency interval; 
is an imaginary unit.
In case, when average individual movement speed in the informative space does not depend on the coordinate 
, the equation (1) looks like:
(3)
and the general solution of (2) can easily be transformed to:
(4)
where 
is a wave number; C(ω) is the integration constant; αω is intial phase for frequency ω.
On the other hand, (3) directly leads to the fact that its solution is the function of the argument 
, or, exactly:
(5)
It becomes certain, if we place (5) in equation (3). Therefore, the solutions of (4) and (5) are equal. An evident form of the distribution function can be found from (3) if the initial probability density distribution of 
. In a close investigation of a weak interaction between students we can use the additivity of individual distribution functions and find a distribution function for a stident group or a stream [3].
The research of the experimentally-found individual distribution functions of a higher education institution students [3] showed that their mathematical expectations move within the informative space with a constant speed (for «strong» students within the whole education period, and for «average» and «weak» students with different constant speed indexes on younger and higher courses). The coordinate in the informative space was evaluated in points. The distribution function was defined in re-calculation for one education discipline per semester. Mathematical expectation was found according to the formula:
It is shown, that the movement of mathematical expectation in the informative space depends on the intensity of a student´s interaction with a professor-tutor personnel.
Movement equation
In article [3] an equation of mathematical expectation movement for individual distribution functions was found. It looks as follows:
(6)
where 
is the function of a student´s knowledge mastering; 
is the totality of parameters that define a student´s ability to master knowledge (intellectual development, psychological and physical health, potential abilities, etc); {Ψ} is the functional from the distribution function ; 
is the function of a professor-tutor personnel impact upon a students´ subsystem; 
is the totality of parameters that characterize professional and personal traits of a professor-tutor personnel.
According to (6) the speed of mathematical expectation movement in the informative space is defined by the actual interaction of student with a professor-tutor personnel. The equation (6) can be transformed into:
(7)
where 
is the function that characterize an individual unmanageableness (inertness) to an alteration of his location in the informative space. Equation (7) is in fact an analogue of Aristotle´s movement equation in mechanics, the power role in which is carried out by the impact function 
, and mass - by the inertness function 
.
To obtain an information on characteristics of the impact function and inertness function it is necessary to carry out some deep pedagogical, psychological, and social researches of the professor-tutor and student subsystem. If we know a specific form of the impact and inertness function, we will be able to find speeds of mathematical expectation of individual distribution functions in the informative space.
Resume
1. A man´s knowledge, being a product of his mind, carry some uncertainty and randomness characteristics, so, it proves impossible to measure a students´ knowledge volume and deepness. To solve this problem we suggest using the probabilistic-statistic method.
2. Within an education process an individual moves within an informative space, where he is defined by a distribution function that defines the probability of his location in a singular volume of the informa-
tive space.
3. According to the solution of the continuity equation we have found an analytical form of a student´s distribution function that spreads in the informative space in time for the case of an average speed random dependence on a coordinate.
4. A speed of individual distribution functions´ mathematical expectation movement speed in the informative space is proportional to a function of a professor-tutor personnel impact and inversely proportional to an inertness function that characterizes an unmanageableness the mathematical expectation in space alteration.
Reference
- Romanov V.P., Sokolova N.A. Probabilistic-statistic model of a student // Modern problems of science and education. - 2009. - № 6 (Part 3). - P. 122-129.
- Sokolova N.A. Education process: determination and randomness // International magazine of applied and fundamental research. - 2010. - №12. - P. 81-82.
- Romanov V.P., Sokolova N.A. The analysis of students´ behavior within an education process in a higher educational institution // Modern problems of science and education. - 2009. - №6 (Part 3. - P. 130-135.